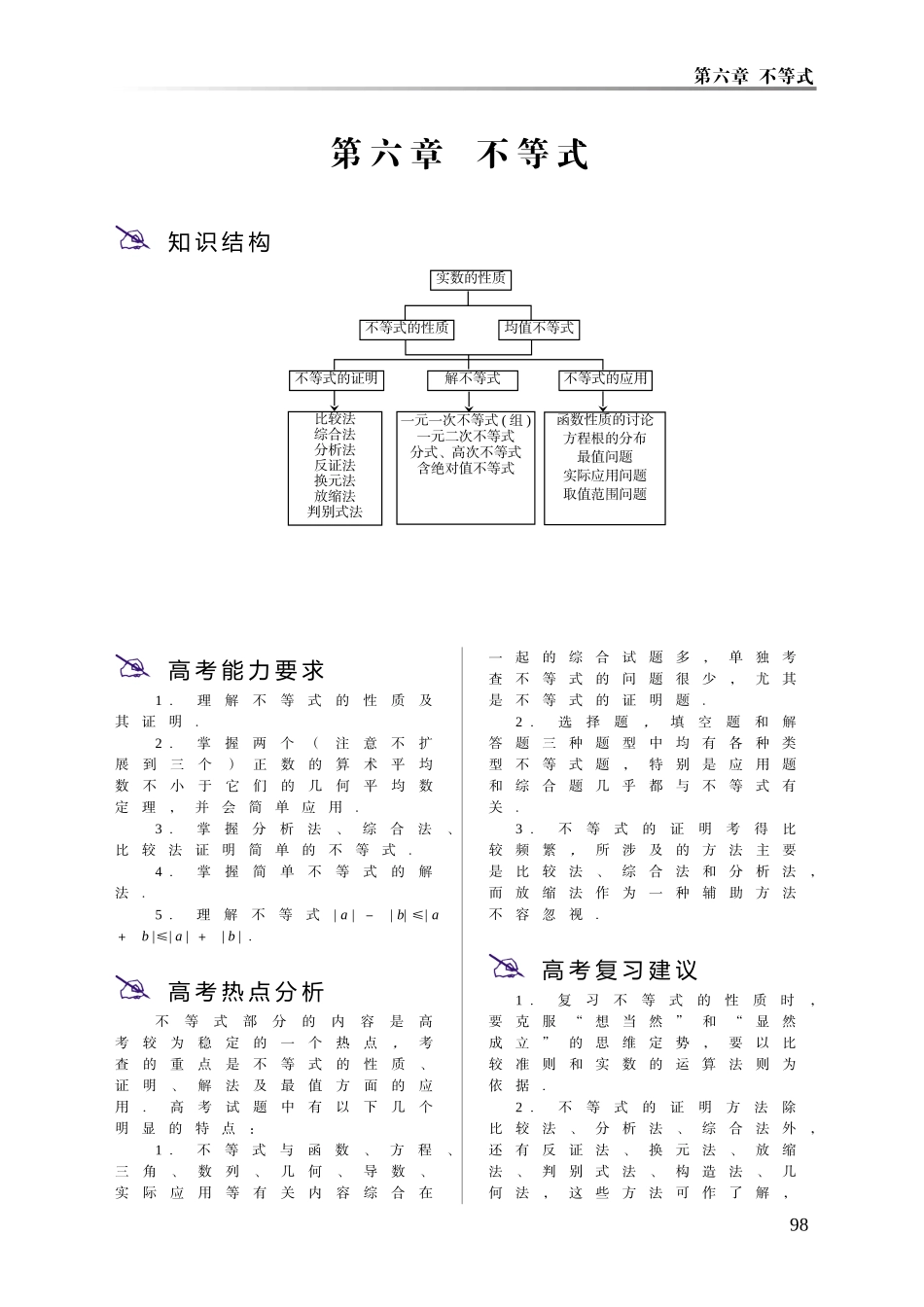
第六章 不等式第 六 章 不 等 式 知 识 结 构 高 考 能 力 要 求1 .理解不等式的性质及其证明.2 .掌握两个(注意不扩展到三个)正数的算术平均数不小于它们的几何平均数定理,并会简单应用.3 .掌握分析法、综合法、比较法证明简单的不等式.4 .掌握简单不等式的解法.5 .理解不等式| a | -| b| ≤| a+b |≤| a | +| b | . 高 考 热 点 分 析不等式部分的内容是高考较为稳定的一个热点,考查的重点是不等式的性质、证明、解法及最值方面的应用.高考试题中有以下几个明显的特点:1 .不等式与函数、方程、三角、数列、几何、导数、实际应用等有关内容综合在一起的综合试题多,单独考查不等式的问题很少,尤其是不等式的证明题.2 .选择题,填空题和解答题三种题型中均有各种类型不等式题,特别是应用题和综合题几乎都与不等式有关.3 .不等式的证明考得比较频繁,所涉及的方法主要是比较法、综合法和分析法,而放缩法作为一种辅助方法不容忽视. 高 考 复 习 建 议1 .复习不等式的性质时,要克服“想当然”和“显然成立”的思维定势,要以比较准则和实数的运算法则为依据.2 .不等式的证明方法除比较法、分析法、综合法外,还有反证法、换元法、放缩法、判别式法、构造法、几何法,这些方法可作了解,98实数的性质不等式的性质均值不等式不等式的证明解不等式不等式的应用比较法综合法分析法反证法换元法放缩法判别式法一元一次不等式 ( 组 )一元二次不等式分式、高次不等式含绝对值不等式函数性质的讨论方程根的分布最值问题实际应用问题取值范围问题高考复习指导丛书 · 数学但要控制量和度.3 .解(证)某些不等式时,要把函数的定义域、值域和单调性结合起来.4 .注意重要不等式和常用思想方法在解题中的作用.5 .利用平均值定理解决问题时,要注意满足定理成立的三个条件:“一正、二定、三相等”.6 .对于含有绝对值的不等式(问题),要紧紧抓住绝对值的定义实质,充分利用绝对值的几何意义.7 .要强化不等式的应用意识,同时要注意到不等式与函数方程的对比与联系.6.1 不等式的概念和性质 知 识 要 点1 、实数的大小比较法则:设a ,b∈R,则a>b ;a=b ;a