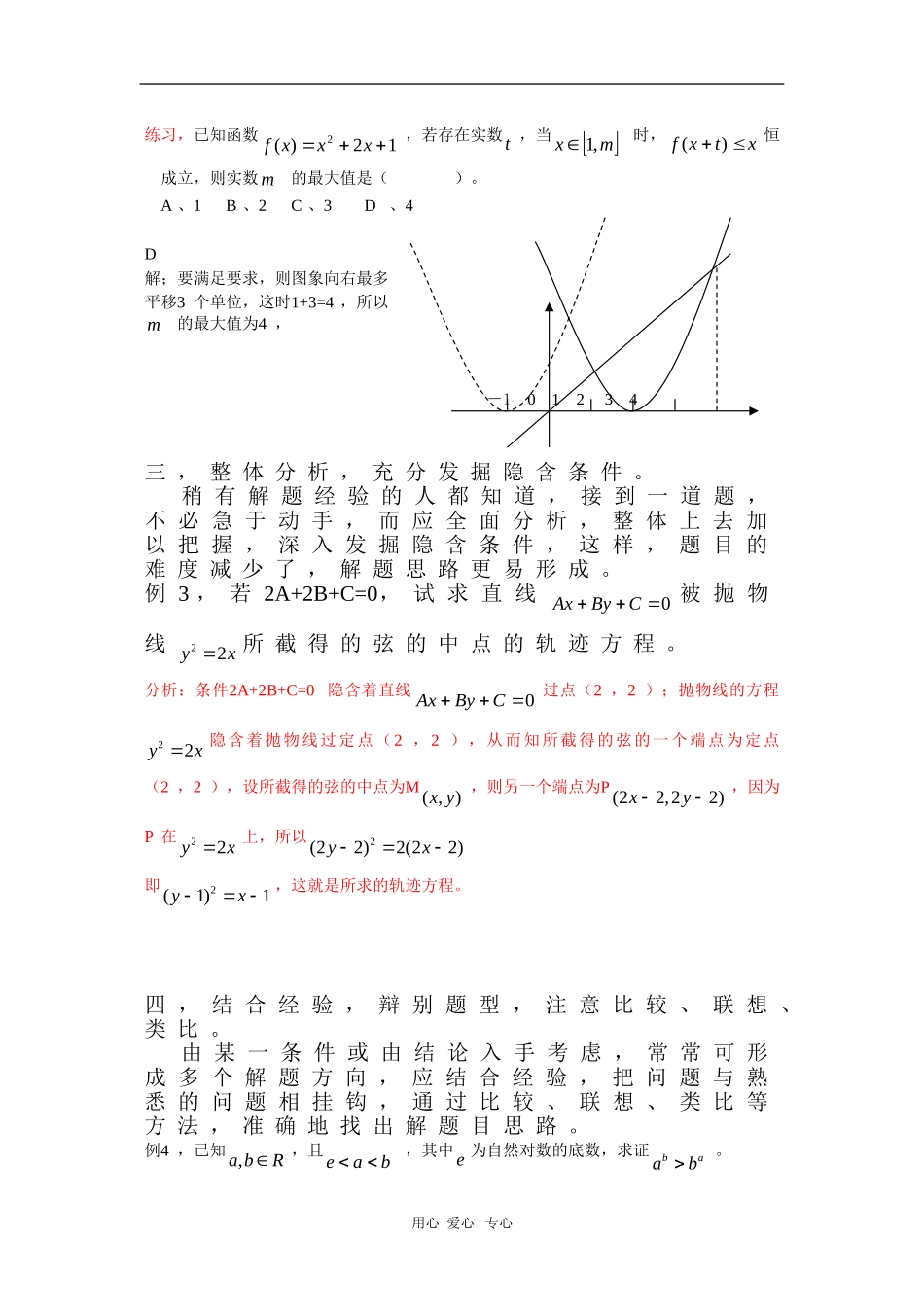
2010 年 高 考 数 学 教 案 : 谈 解 题 思 路 的 形 成著 名 数 学 教 育 家 波 利 亚 说 过 : “ 掌 握 数 学意 味 着 什 么 ? 这 就 是 说 , 善 于 解 题 。 ” 解 题的 关 键 是 尽 快 的 、 准 确 地 找 到 解 题 的 思 路 ,在 解 答 数 学 题 时 , 如 何 才 能 形 成 思 路 呢 ? 下面 对 这 个 问 题 作 一 些 探 索 。一 ,抓 住 要 点 , 形 成 思 路学生碰到题型新颖,有一定难度的数学题时,往往会思路受阻,无法做下去,这时需冷静分析,研究问题到底“卡”在哪里?这个“卡”就是问题的要点。例1 ,设12(1)( )lgxxxnn af xn,其中a 是实数,n 是自然数,且2n ,当(,1]x 时,若( )f x有意义,求a 的取值范围。分析:依题意知,当2n 且(,1]x 时,有121)0xxxnn a (于是,121[( )( )() ]xxxnannn ,记 ( )g x 121[( )( )() ]xxxnnnn问题的要点在于:求a 的取值范围,实质上须求 ( )g x的最大值M,a M,易证 ( )g x在(,1] 上是增函数,右可得:M12n ,故12na 。二 , 借 助 图 形 , 寻 找 突 破 口数学中很多问题都具有“形”的因素,如果能给数学命题以直观,形象的图形描述,就可化抽象为形象,化难为易,形成解题的思路。例2 ,求函数( )32cos2sin22cosf 的最小值。分析:本题有一定的难度,一般方法不易解,注意到22sincos1,可得:2222( )(cos1)(sin1)(cos1)sinf ,即求点M(cos ,sin )到点P(1,1) 与点Q( 1,0)的距离的和的最小值。因为点M为单位圆上的动点,因此,即求圆上的动点M到P ,Q 距离的和的最小值(如图),易得该最小值为 5 。用心 爱心 专心PQ练习,已知函数12)(2xxxf,若存在实数t ,当mx,1时,xtxf )(恒成立,则实数m的最大值是( )。A 、1 B 、2 C 、3 D 、4 D解;要满足要求,则图象向右最多平移3 个单位,这时1+3=4 ,所以m的最大值为4 ,-1 0 1 2 3 4 三 , 整 体 分 析 , 充 分 发 掘 隐 含 条 件 。 稍 有 解 题 经 验 的 人 都 知 道 , 接 到 一 道 题 ,不 必 急 于 动 手 , ...