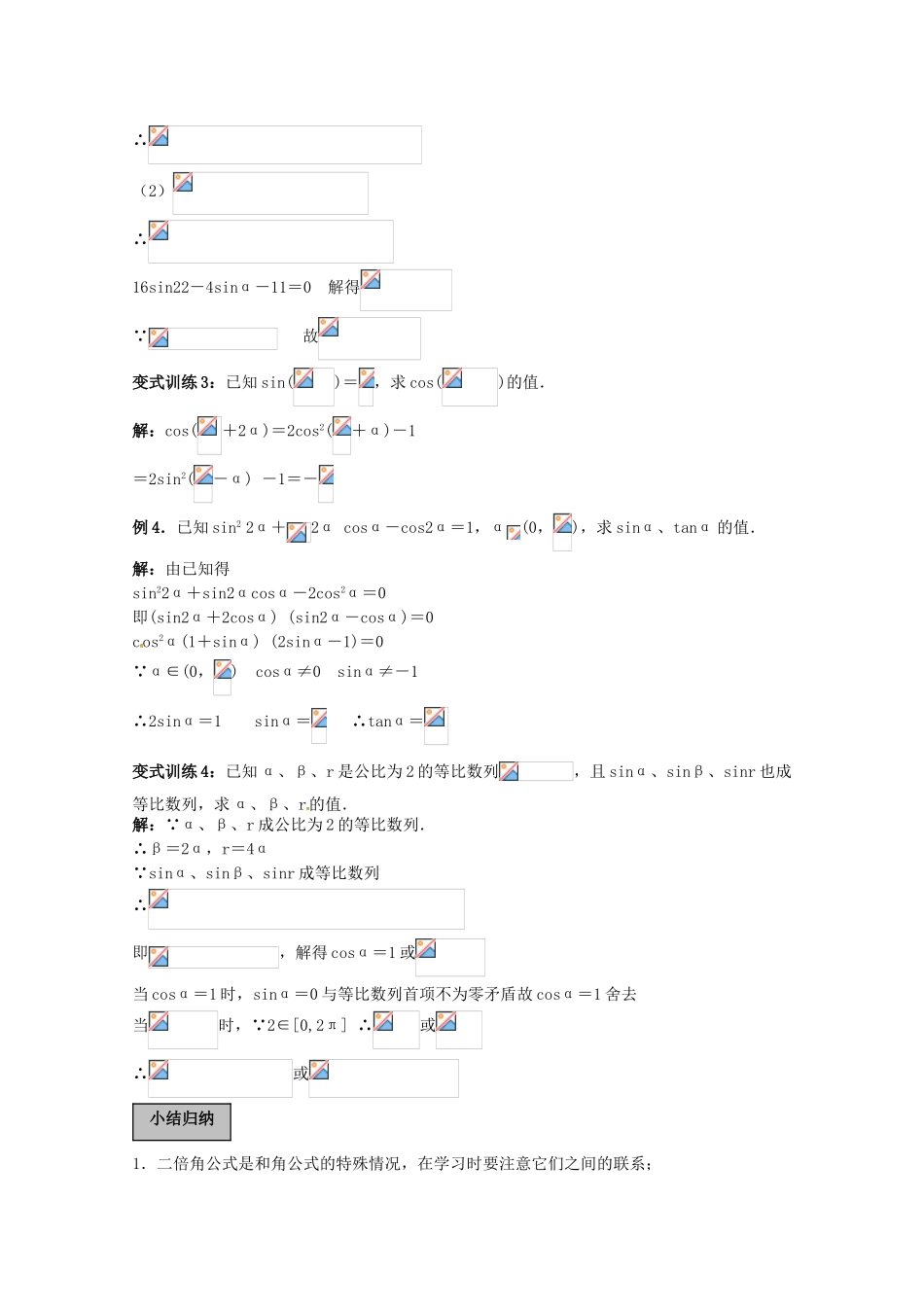
第 4 课时 二倍角的正弦、余弦、正切1.基本公式:sin2α= ;cos2α= = = ;tan2α= .2.公式的变用:1+cos2α= ;1-cos2α= .例 1. 求值:解:原式= ==变式训练 1:(cos+sin)= ( )A.- B.- C. D. 解:D例 2. 已知 α 为锐角,且,求的值. 解: α 为锐角∴====变式训练 2:化简:解:原式==1例 3.已知;(1) 求的值; (2) 设,求 sinα 的值.解:(1) 典型例题基础过关∴(2)∴16sin22-4sinα-11=0 解得 故变式训练 3:已知 sin()=,求 cos()的值.解:cos(+2α)=2cos2(+α)-1=2sin2(-α) -1=-例 4.已知 sin2 2α+2α cosα-cos2α=1,α(0,),求 sinα、tanα 的值.解:由已知得sin22α+sin2αcosα-2cos2α=0即(sin2α+2cosα) (sin2α-cosα)=0cos2α(1+sinα) (2sinα-1)=0 α∈(0,) cosα≠0 sinα≠-1∴2sinα=1 sinα= ∴tanα=变式训练 4:已知 α、β、r 是公比为 2 的等比数列,且 sinα、sinβ、sinr 也成等比数列,求 α、β、r的值.解: α、β、r 成公比为 2 的等比数列.∴β=2α,r=4α sinα、sinβ、sinr 成等比数列∴即,解得 cosα=1 或当 cosα=1 时,sinα=0 与等比数列首项不为零矛盾故 cosα=1 舍去当时, 2∈[0,2π] ∴或∴或1.二倍角公式是和角公式的特殊情况,在学习时要注意它们之间的联系;小结归纳2.要理解二倍角的相对性,能根据公式的特点进行灵活应用(正用、逆用、变形用).3.对三角函数式的变形有以下常用的方法:① 降次(常用降次公式)② 消元(化同名或同角的三角函数)③ 消去常数“1”或用“1”替换④ 角的范围的确定第 5 课时 三角函数的化简和求值1.三角函数式的化简的一般要求: ① 函数名称尽可能少;② 项数尽可能少;③ 尽可能不含根式;④ 次数尽可能低、尽可能求出值.2.常用的基本变换方法有:异角化同角、异名化同名、异次化同次.3.求值问题的基本类型及方法① “给角求值”一般所给的角都是非特殊角,解题时应该仔细观察非特殊角与特殊角之间的关系,通常是将非特殊角转化为特殊角或相互抵消等方法进行求解.② “给值求值”即给出某些角的三角函数(式)的值,求另外的一些角的三角函数值,解题关键在于:变角,使其角相同;③ “给值求角”关键也是:变角,把所求的角用含已知角的式子表示,由所求得的函...