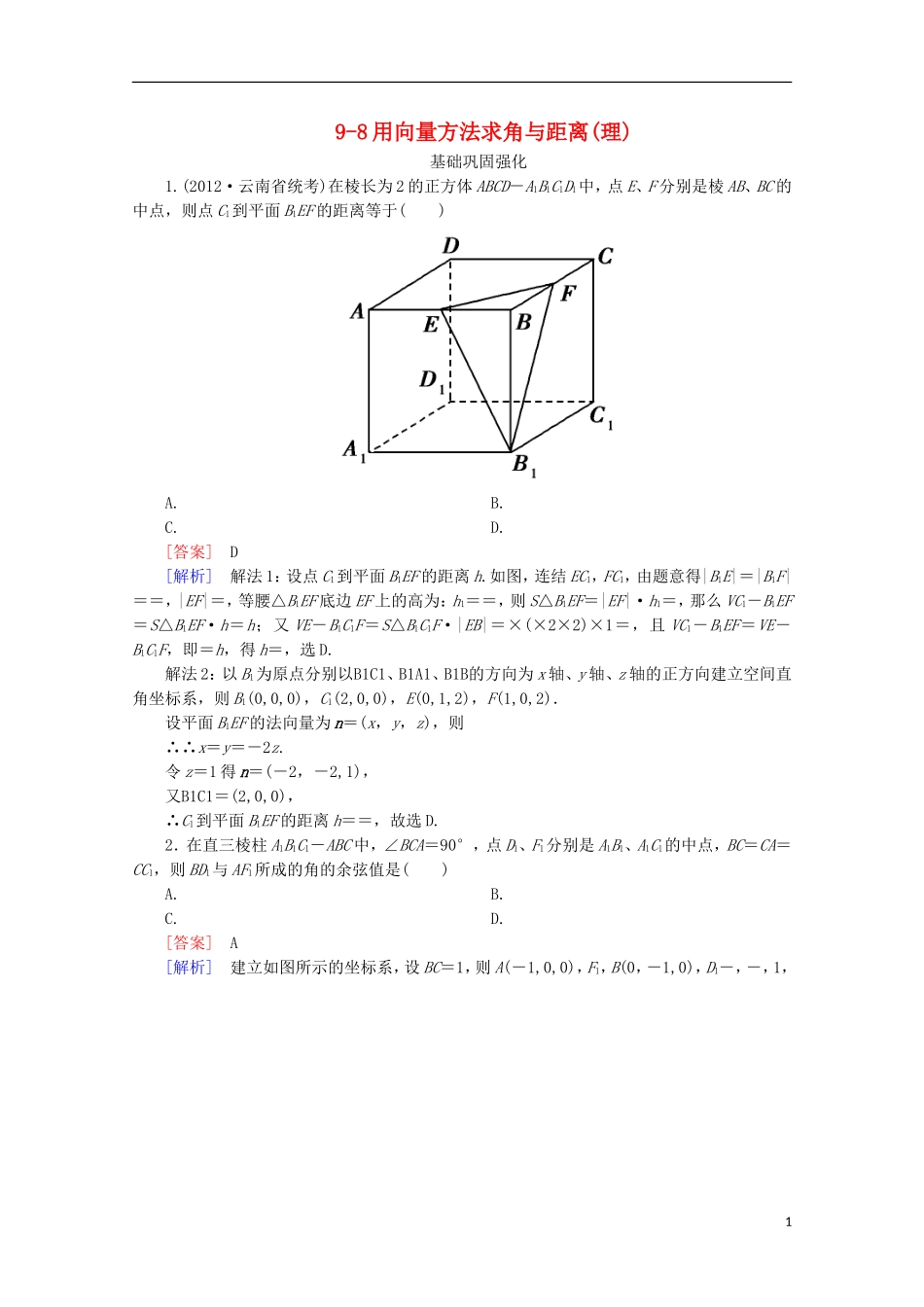
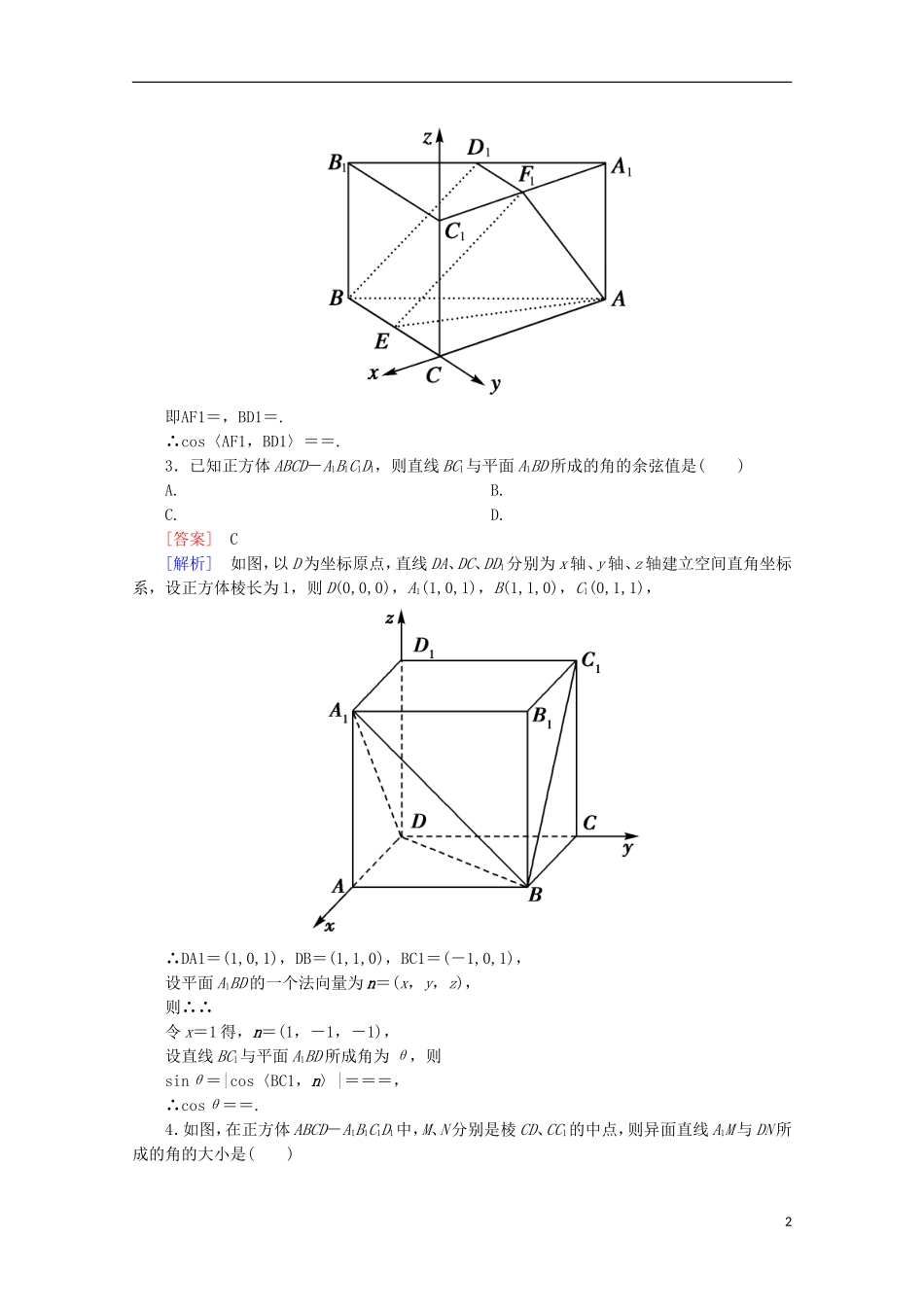
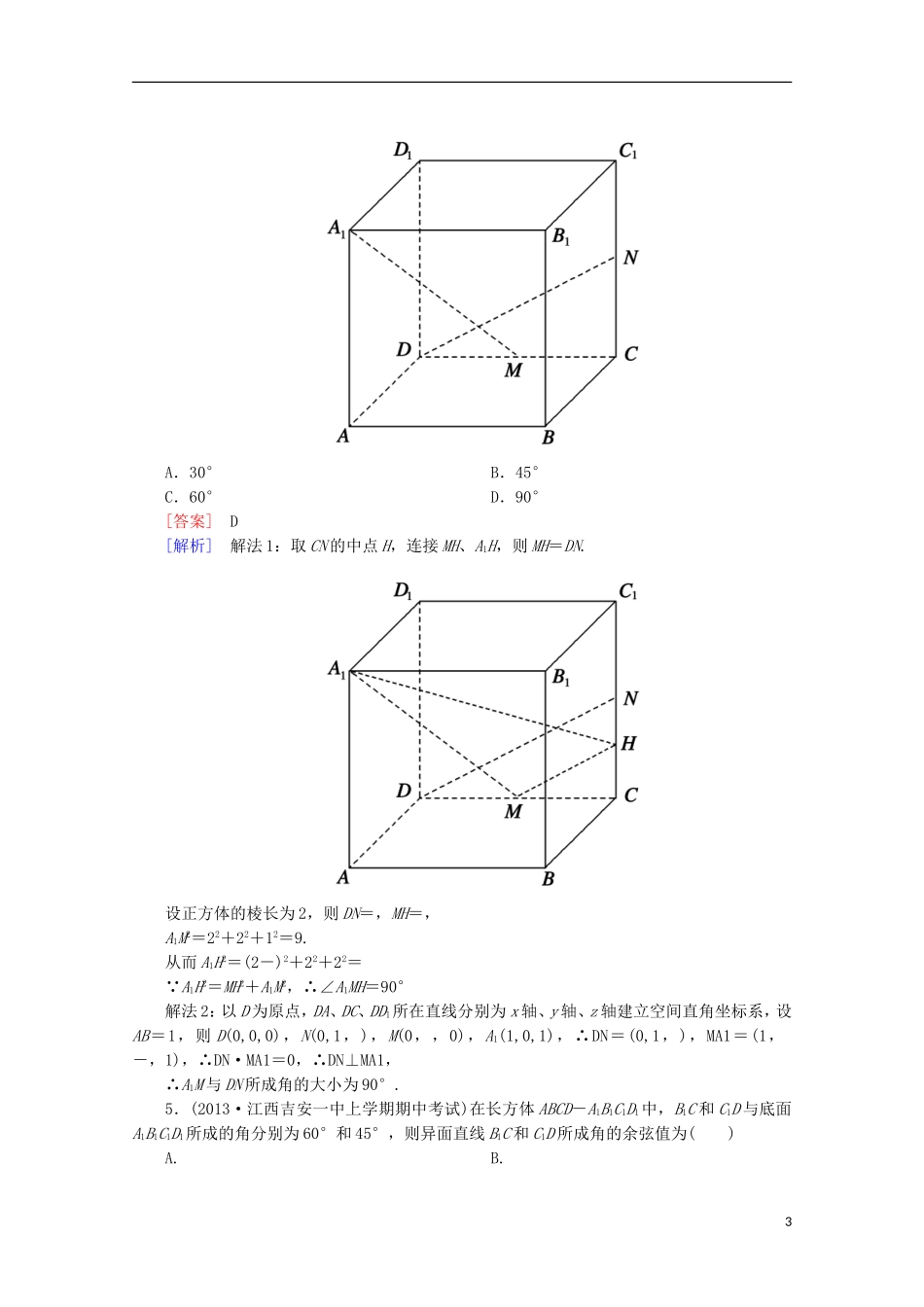
9-8 用向量方法求角与距离(理)基础巩固强化1.(2012·云南省统考)在棱长为 2 的正方体 ABCD-A1B1C1D1中,点 E、F 分别是棱 AB、BC 的中点,则点 C1到平面 B1EF 的距离等于( )A. B.C. D.[答案] D[解析] 解法 1:设点 C1到平面 B1EF 的距离 h.如图,连结 EC1,FC1,由题意得|B1E|=|B1F|==,|EF|=,等腰△B1EF 底边 EF 上的高为:h1==,则 S△B1EF=|EF|·h1=,那么 VC1-B1EF=S△B1EF·h=h;又 VE-B1C1F=S△B1C1F·|EB|=×(×2×2)×1=,且 VC1-B1EF=VE-B1C1F,即=h,得 h=,选 D.解法 2:以 B1为原点分别以B1C1、B1A1、B1B的方向为 x 轴、y 轴、z 轴的正方向建立空间直角坐标系,则 B1(0,0,0),C1(2,0,0),E(0,1,2),F(1,0,2).设平面 B1EF 的法向量为 n=(x,y,z),则∴∴x=y=-2z.令 z=1 得 n=(-2,-2,1),又B1C1=(2,0,0),∴C1到平面 B1EF 的距离 h==,故选 D.2.在直三棱柱 A1B1C1-ABC 中,∠BCA=90°,点 D1、F1分别是 A1B1、A1C1的中点,BC=CA=CC1,则 BD1与 AF1所成的角的余弦值是( )A. B.C. D.[答案] A[解析] 建立如图所示的坐标系,设 BC=1,则 A(-1,0,0),F1,B(0,-1,0),D1-,-,1,1即AF1=,BD1=.∴cos〈AF1,BD1〉==.3.已知正方体 ABCD-A1B1C1D1,则直线 BC1与平面 A1BD 所成的角的余弦值是( )A. B.C. D.[答案] C[解析] 如图,以 D 为坐标原点,直线 DA、DC、DD1分别为 x 轴、y 轴、z 轴建立空间直角坐标系,设正方体棱长为 1,则 D(0,0,0),A1(1,0,1),B(1,1,0),C1(0,1,1),∴DA1=(1,0,1),DB=(1,1,0),BC1=(-1,0,1),设平面 A1BD 的一个法向量为 n=(x,y,z),则∴∴令 x=1 得,n=(1,-1,-1),设直线 BC1与平面 A1BD 所成角为 θ,则sinθ=|cos〈BC1,n〉|===,∴cosθ==.4.如图,在正方体 ABCD-A1B1C1D1中,M、N 分别是棱 CD、CC1的中点,则异面直线 A1M 与 DN 所成的角的大小是( )2A.30° B.45°C.60° D.90°[答案] D[解析] 解法 1:取 CN 的中点 H,连接 MH、A1H,则 MH=DN.设正方体的棱长为 2,则 DN=,MH=,A1M2=22+22+12=9.从而 A1H2=(2-)2+22+22= A1H2=MH2+A1M2,∴∠A1MH=90°解法 2:以 D 为原点,DA、DC、DD1所在直线分别为 x 轴、y 轴、z 轴建立空间直角坐标系,设AB=1,则 D(0,0,0),N(0,1,),M(0,,0...