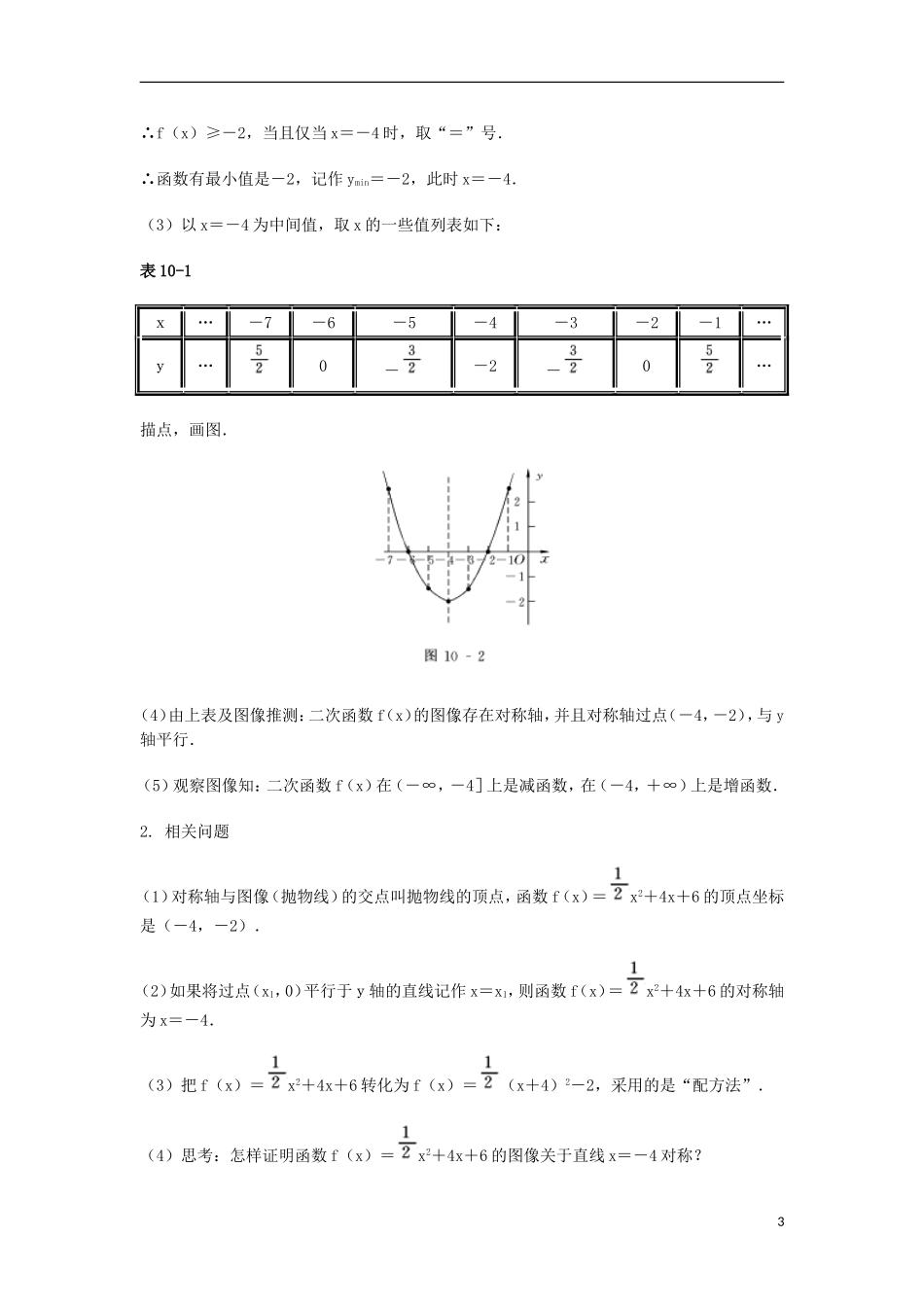
10 二 次 函 数教材分析二次函数是重要的基本函数之一,由于它存在最值,因此,其单调性在实际问题中有广泛的应用,并且它与前面学过的二次方程有密切联系,又是后面学习解一元二次不等式的基础.二次函数在初中学生已学过,主要是定义和解析式,这里,在此基础上,接着学习二次函数的性质与图像,进而使学生对二次函数有一个比较完整的认识.本节先研究特殊的二次函数 y=ax2,(a≠0)的图像与 a 值的关系,这可通过 a 在 0 的附近取值画图观察得到.然后,通过一个实例,如 y=x2+4x+6,研讨二次函数的性质与图像.最后,总结出一般性结论.这节内容的重点是二次函数的性质,即顶点坐标、对称轴方程、二次函数的单调性及其图像,难点是用配方法把 y=ax2+bx+c 的形式转化为 y=a(x-h)2+k 的形式.教学目标1. 通过一个例子研究二次函数的图像和性质,得到一般性结论,培养学生归纳、抽象能力.2. 掌握二次函数的概念、表达式、图像与性质.会用配方法解决有关问题,能熟练地求二次函数的最值.3. 能初步运用二次函数解决一些实际问题,培养学生分析问题和解决问题的能力.任务分析学习这节内容时要先复习一下学生初中学过的二次函数的有关问题.为了得到 y=ax2,(a≠0)的图像与 a 的关系以及二次函数 y=ax2+bx+c 的性质,这里遵循由特例到一般的原则,充分利用图像的直观性,以便学生接受.在这一过程中,应讲明配方法的操作过程.教学设计一、复习引申1. 什么是二次函数?2. 在同一坐标系中作出下列函数的图像.(1)y=-3x2. (2)y=-2x2. (3)y=-x2. (4)y=-0.5x2.(5)y=0.5x2. (6)y=x2.(7)y=2x2. (8)y=3x2.13. 学生讨论:函数 y=ax2中系数 a 的取值与它的图像形状有何关系?4. 教师明晰:在 a 从-3 逐渐变化到+3 的过程中,抛物线开口向下并逐渐变大,当 a=0 时,y=0,抛物线变为 x 轴,然后抛物线开口向上,并逐渐变小.二、问题情境已知二次函数 f(x)=x2+4x+6.(1)求它与 x 轴的交点坐标.(2)问:它有没有最值?若有最大(小)值,最大(小)值是多少?试求出此时对应的自变量x的值.(3)画出它的图像.(4)它的图像有没有对称轴?如果有,位置如何?(5)确定函数的单调区间.1. 先让学生独立解答问题 1,然后师生共同确定答案(1)令 y=0,即x2+4x+6=0,解得 x1=-6,x2=-2.∴与x轴交于两点(-6,0),(-...