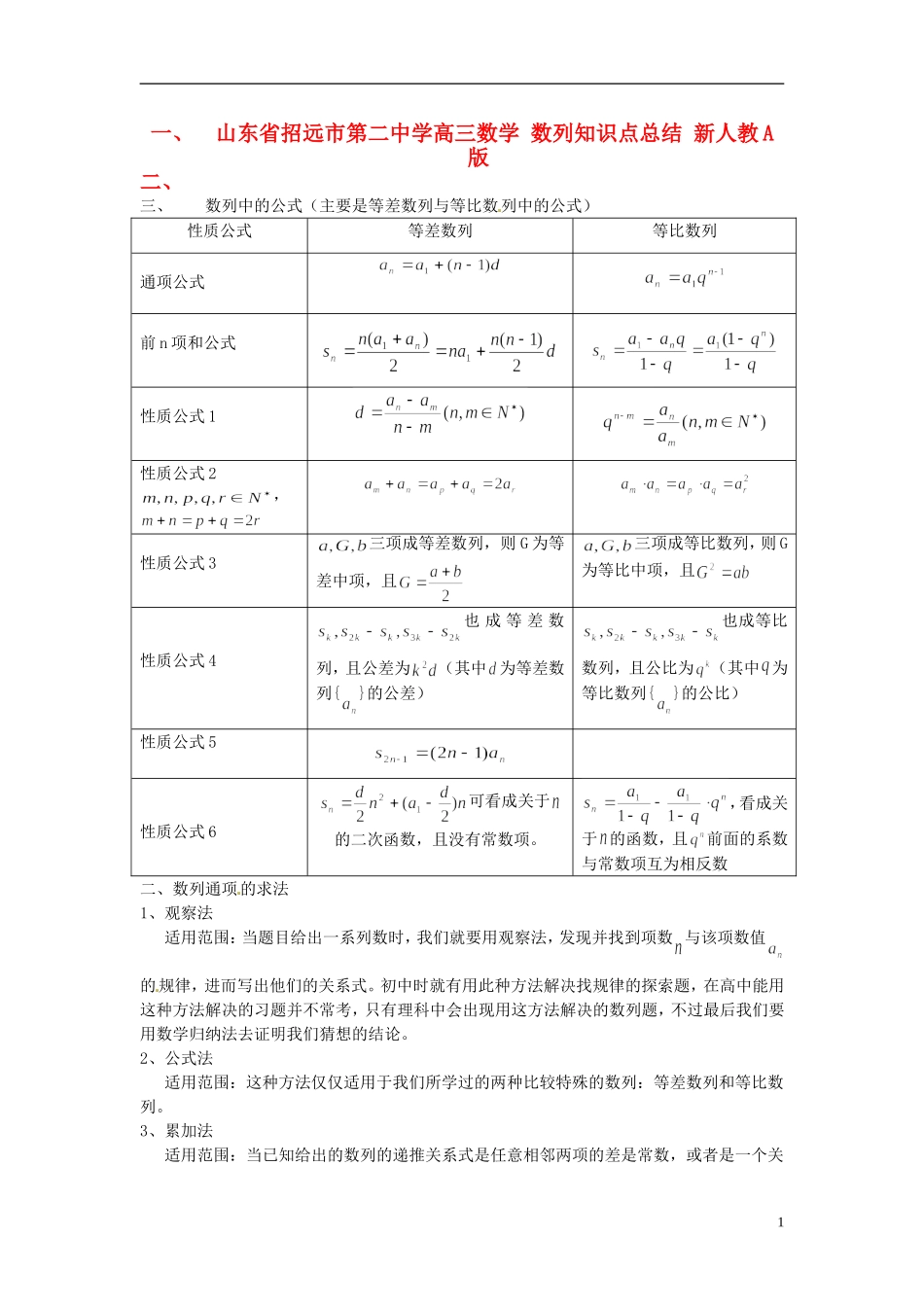
一、山东省招远市第二中学高三数学 数列知识点总结 新人教 A版二、三、数列中的公式(主要是等差数列与等比数列中的公式)性质公式等差数列等比数列通项公式前 n 项和公式性质公式 1性质公式 2,性质公式 3三项成等差数列,则 G 为等差中项,且三项成等比数列,则 G为等比中项,且性质公式 4也 成 等 差 数列,且公差为(其中 为等差数列{}的公差)也成等比数列,且公比为(其中 为等比数列{}的公比)性质公式 5性质公式 6可看成关于的二次函数,且没有常数项。,看成关于 的函数,且前面的系数与常数项互为相反数二、数列通项的求法1、观察法 适用范围:当题目给出一系列数时,我们就要用观察法,发现并找到项数 与该项数值的规律,进而写出他们的关系式。初中时就有用此种方法解决找规律的探索题,在高中能用这种方法解决的习题并不常考,只有理科中会出现用这方法解决的数列题,不过最后我们要用数学归纳法去证明我们猜想的结论。2、公式法 适用范围:这种方法仅仅适用于我们所学过的两种比较特殊的数列:等差数列和等比数列。3、累加法 适用范围:当已知给出的数列的递推关系式是任意相邻两项的差是常数,或者是一个关1于 的函数,都可用累加法求出该数列的通项公式。4、累乘法 适用范围:当已知给出的数列的递推关系式是任意相邻两项的商是常数,或者是一个关于 的函数,都可用累乘法求出该数列的通项公式。5:、利用与的关系式求数列通项 适用范围:只要已知给出的递推关系式中含有或者,之类的式子,都可以用这种方法求解通项公式,要注意的是:得分开来讨论。6、构造法(主要是两种题型) 使用范围:(1)形如或者形式的数列可用构造法,其中是常数,是关于 的一次函数或者是幂函数。 (2)形如或者变式形式的数列可用构造法,其中是常数。三、数列前 项和的求法1、公式法 适用范围:当已知给出的数列是等差数列或者是等比数 列时,都可用公式法求其前 项的和。2、裂项相消 适用范围:形如,或者形式的数列可用裂项相消法。注意在运用裂项相消法求数列的前 项和时,必须要先把通项裂开,这样求和时,计算也会简单很多,可以节省不少的时间。3、错位相减 适用范围:形如(其中是等差数列, 是等比数列)形式的数列,就可用裂项相消法求通项,且只能用这种方法去求。这种方法的解题关键是个人计算能力的高低,计算中细心点,相信问题很快便会迎刃而解。4、分组求和 适用范围:形如(其中是常数,则...