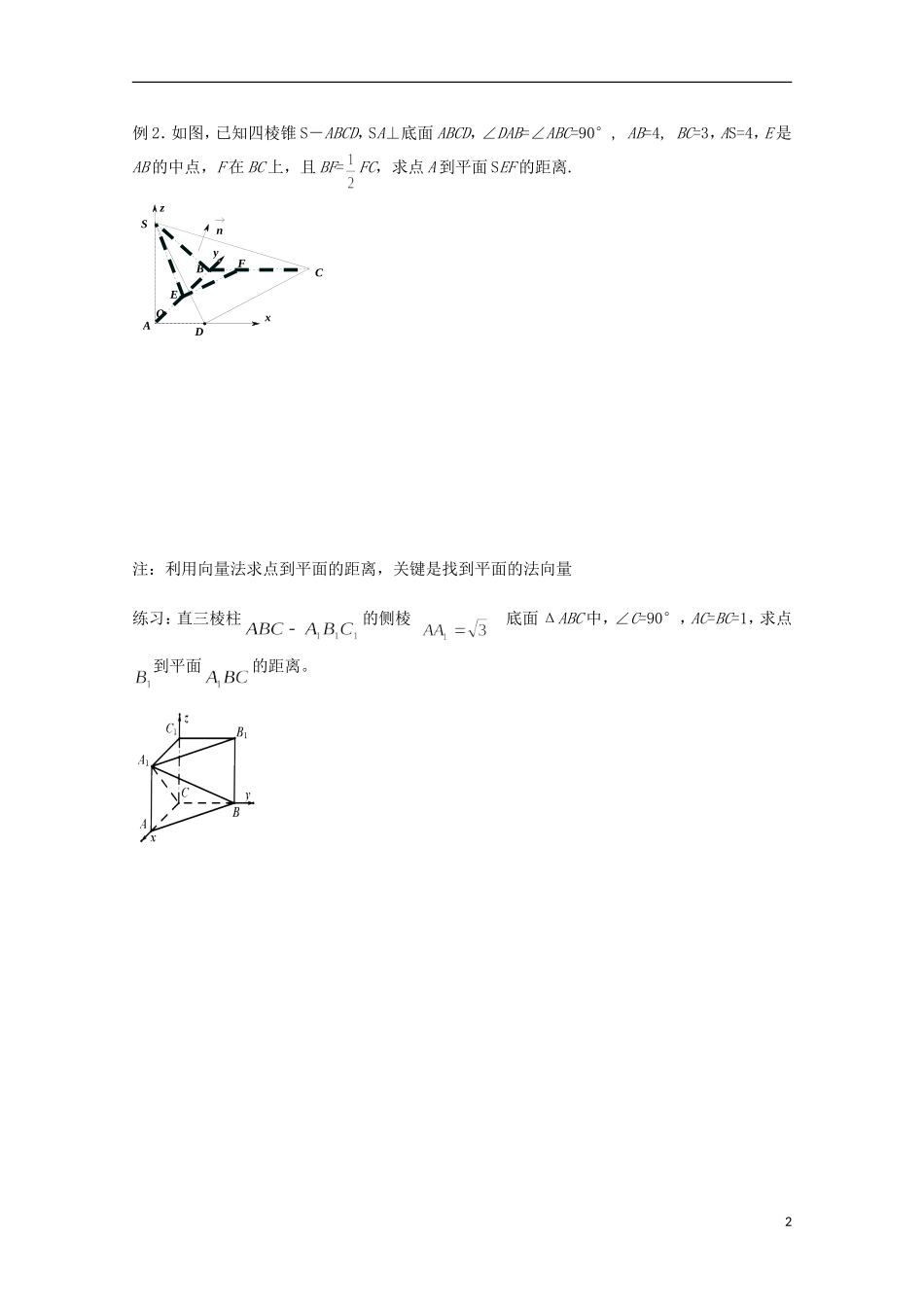
山东省济南市章丘中学高二数学《距离》学案学习目标1. 掌握点到平面的距离的概念,并会求点到平面的距离.2.能利用直线的方向向量和平面的法向量求空间中的各种距离.3.体会向量方法在研究立体几何中的作用知识梳理1.距离的概念:一个图形内的任一点与另一个图形内的任一点的距离中的 ,叫做图形与图形之间的距离。计算任何图形之间的距离都可以转化为求两点之间的距离。2.点到平面的距离 :一点到它在一个平面内的 的距离叫做点到这个平面的距离。3.直线与平行平面的距离:一条直线上的任一点,与 叫做直线与平面的距离。4.两个平行平面的距离:和两个平行平面 的直线,叫做两个平面的公垂线,公垂线夹在平行平面间的部分,叫做 。两平行平面的 叫做两平行平面的距离。典例解析例1.已知平行六面体ABCD-A’B’C’D’,AB=4,AD=3,AA’=5,∠BAD=90°,∠BAA’=∠ DAA’=60° ,求 AC’的长。 变式练习 :已知二面角为 45 度,点 A 在平面 内,点 A 到棱 的距离等于 a,求点 A 到平面的距离_D'_C'_B'_A'_D_C_B_A1例 2.如图,已知四棱锥 S-ABCD,SA⊥底面 ABCD,∠DAB=∠ABC=90°, AB=4, BC=3,AS=4,E 是AB 的中点,F 在 BC 上,且 BF=FC,求点 A 到平面 SEF 的距离.注:利用向量法求点到平面的距离,关键是找到平面的法向量练习:直三棱柱的侧棱 底面 ΔABC 中,∠C=90°,AC=BC=1,求点到平面的距离。EOFSzyx nDCBA2课堂小结:因此要求一个点到平面的距离,可分以下几步完成: (1)求出该平面的一个法向量; (2)找出从该点出发到平面的任一条斜线段对应的向量. (3)求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即可求出点到平面的距离.由于 n|n|=n0 可以视为平面的单位法向量,所以点到平面的距离实质就是平面的单位法向量与从该点出发的斜线段向量的数量积的绝对值,即 d=|AB→ ·n0|. 再者:若直线 a∥平面 α,则直线 a 上的任意一点到平面的距离都相等;若平面 α∥平面 β,则平面 α 上任意一点到平面 β 的距离也都相等.因此直线到平面的距离以及两平行平面间的距离都可转化为点到平面的距离解决.反馈练习1. 、 为异面直线,二面角— —,,,如果二面角— —的平面角为 ,则 , 所成的角为( )A. B. C. 或 D.2.一条直线与平面 a 成 60°角,则这条直线与平面内的直线所成角的取值范围是 ( )A.[0°,90°] B....