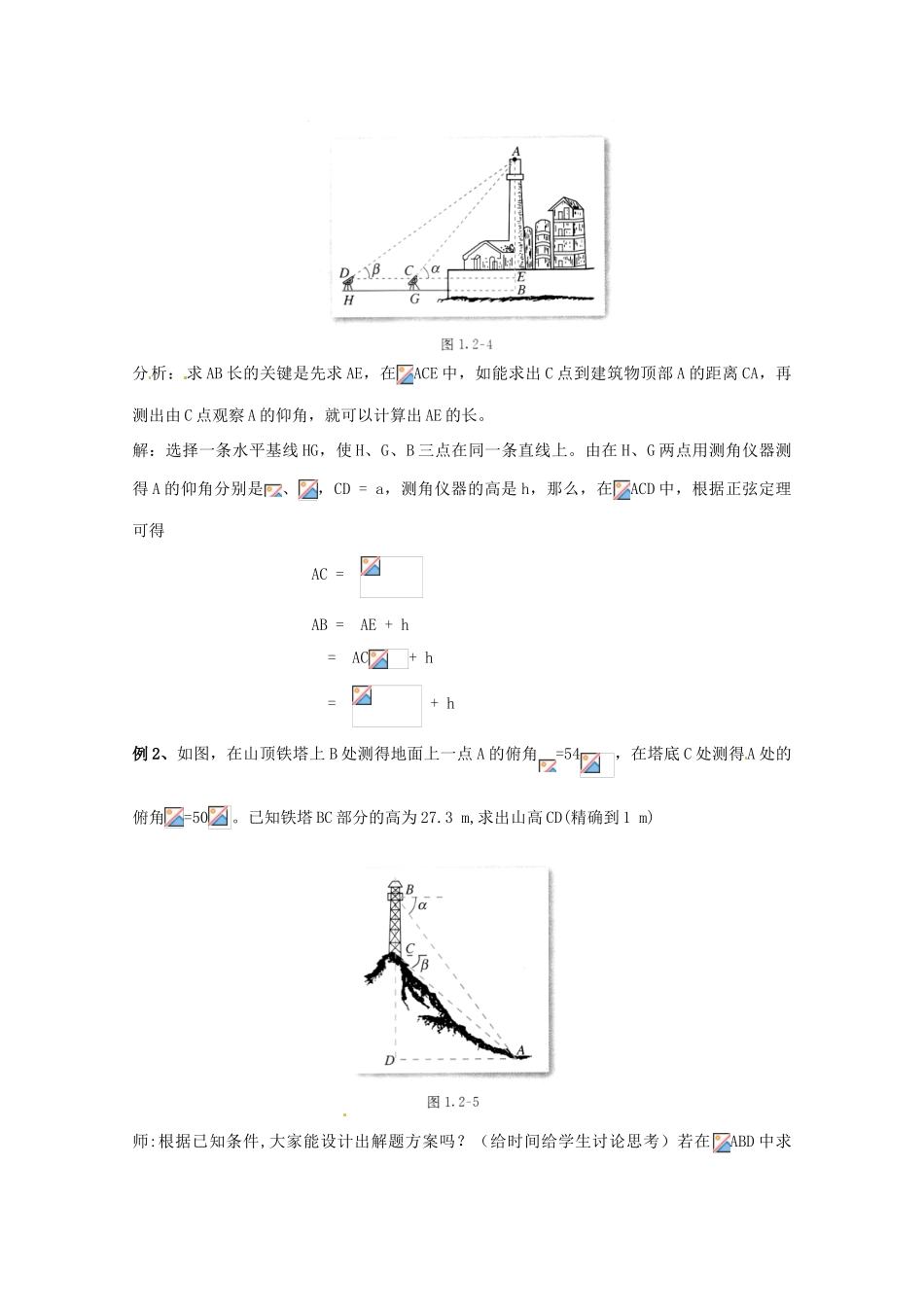
山东省沂水县第一中学高考数学一轮复习学案:解三角形应用举例●三维目标知识与技能:能够运用正弦定理、余弦定理 等知识和方法解决一些有关底部不可到达的物体高度测量的问题过程与方法:本节课是解三角形应用举例的延伸。采用启发与尝试的方法,让学生在温故知新中学会正确识图、画图、想图,帮助学生逐步构建知识框架。通过 3 道例题 的安排和练习的训练来巩固深化解三角形实际问题的一般方法。教学形式要坚持引导——讨论——归纳,目的不在于让学生记住结论,更多的要养成良好的研究、探索习惯。作业设计思考题,提供学生更广阔的思考空间情感态度与价值观:进一步培养学生学习数学、应用数学的意识及观察、归纳、类比、概括的能力●教学重点结合实际测量工具,解决生活中的测量高度问题●教学难点能观察较复杂的图形,从中找到解决问题的关键条件●教学过程Ⅰ.课题导入提问:现实生活中,人 们是怎样测量底部不可到达的建筑物高度呢?又怎样在水平飞行的飞机上测量飞机下方山顶 的海拔高度呢?今天我们就来共同探讨这方面的问题Ⅱ.讲授新课[范例讲解]例 1、AB 是底部 B 不可到达的一个建筑物,A 为建筑物的最高点,设计一种测量建筑物高度AB 的方法。分析: 求 AB 长的关键是先求 AE,在ACE 中,如能求出 C 点到建筑物顶部 A 的距离 CA,再测出由 C 点观察 A 的仰角,就可以计算出 AE 的长。解:选择一条水平基线 HG,使 H、G、B 三点在同一条直线上。由在 H、G 两点用测角仪器测得 A 的仰角分别是、,CD = a,测角仪器的高是 h,那么,在ACD 中,根据正弦定理可得AC = AB = AE + h = AC+ h = + h例 2、如图,在山顶铁塔上 B 处测得地面上一点 A 的俯角=54,在塔底 C 处测得A 处的俯角=50。已知铁塔 BC 部分的高为 27.3 m,求出山高 CD(精确到 1 m)师:根据已知条件,大家能设计出解题方案吗?(给时间给学生讨论思考)若在ABD 中求CD,则关键需要求出哪条边呢?生:需求出 BD 边。师:那如何求 BD 边呢?生:可首先求出 AB 边,再根据BAD=求得。解:在ABC 中, BCA=90 +,ABC =90 -,BAC=- ,BAD =.根据正弦定理, = 所以 AB ==解 RtABD 中,得 BD =ABsinBAD=将测量数据代入上式,得 BD = = ≈177 (m)CD =BD -BC≈177-27.3=150(m)答:山的高度约为 150 米.师:有没有别的解法呢?生:若在ACD 中求 CD,可先求出 AC。师:分析得很好,请大家接着思...