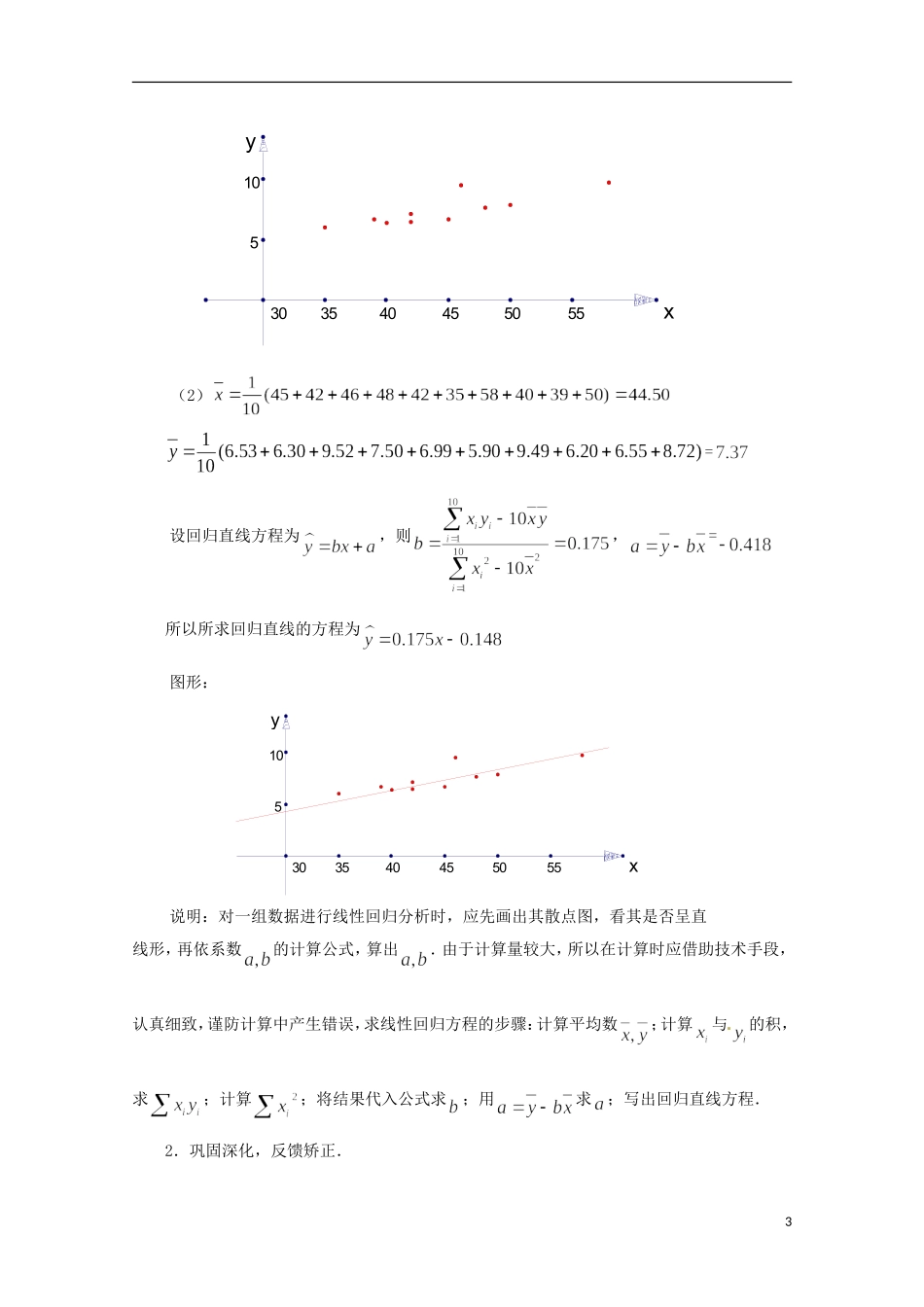
2.4 线性回归方程(2)教学目标:1.了解非确定性关系中两个变量的统计方法;2.掌握散点图的画法及在统计中的作用;3.掌握回归直线方程的求解方法.教学重点:线性回归方程的求解.教学难点:回归直线方程在现实生活与生产中的应用.教学方法:引导发现、合作探究. 教学过程: 一、复习练习1.已知回归方程,则 x=25 时,y 的估计值为 2.三点的线性回归方程是 ( D )A. B. C. D. 3.我们考虑两个表示变量与之间的关系的模型,为误差项,模型如下:模型 1:;模型 2:.(1)如果,分别求两个模型中的值;(2)分别说明以上两个模型是确定性模型还是随机模型.解:(1)模型 1:;模型 2:(2)模型 1 中相同的值一定得到相同的值,所以是确定性模型;模型 2 中相同的值,1因的不同,所得值不一定相同,且为误差项是随机的,所以模型 2 是随机性模型.二、数学运用1.例题讲解.例 1 一个车间为了规定工时定额,需要确定加工零件所花费的时间.为此进行了 10 次试验,测得数据如下:零件个数 (个)102030405060708090100加工时间 (分)626875818995102108115122请判断与是否具有线性相关关系,如果与具有线性相关关系,求线性回归方程.解:在直角坐标系中画出数据的散点图,直观判断散点在一条直线附近,故具有线性相关关系.由测得的数据表可知: ∴ ,因此,所求线性回归方程为例 2 已知 10 只狗的血球体积及红血球数的测量值如下:454246484235584039506.536.309.527.506.995.909.496.206.598.72(血球体积),(红血球数,百万)(1)画出上表的散点图;(2)求出回归直线方程且画出图形.解:(1)2x30y5103540455055(2) =设回归直线方程为,则,=所以所求回归直线的方程为 图形:x30y5103540455055说明:对一组数据进行线性回归分析时,应先画出其散点图,看其是否呈直线形,再依系数的计算公式,算出.由于计算量较大,所以在计算时应借助技术手段,认真细致,谨防计算中产生错误,求线性回归方程的步骤:计算平均数;计算与的积,求;计算;将结果代入公式求;用求;写出回归直线方程.2.巩固深化,反馈矫正. 3(1)下面是南京市与哈尔滨 2001 年 12 个月的月平均气温(单位: C)试分析这两个城市的月平均气温是否具有相关关系,若有,求出线性回归方程;若没有,说明理由.月份123456南京月平均气温2 3.88.414.819.924.5哈尔滨月平均气温-19.4-15.4-4.8614...