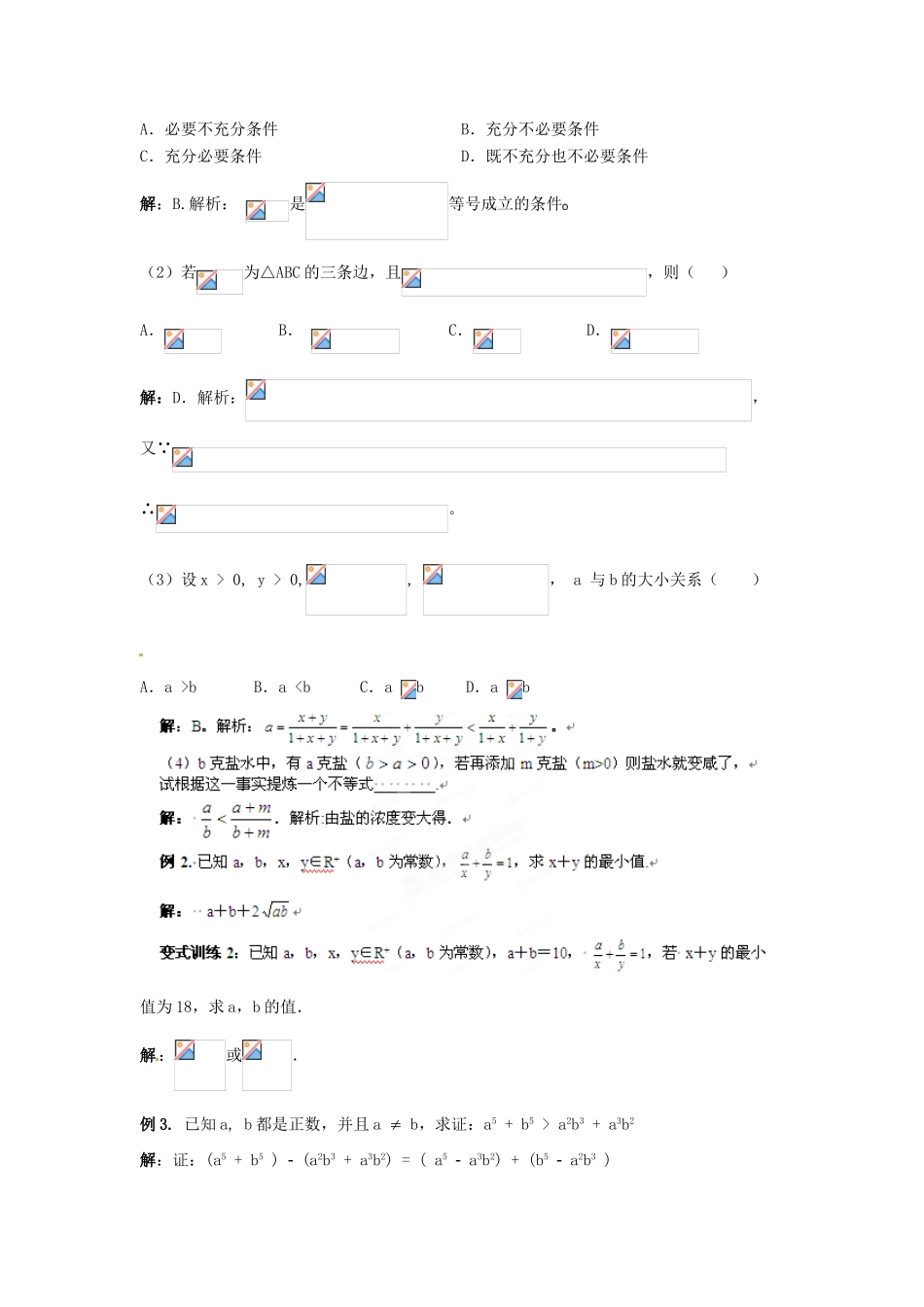
第 2 课时 算术平均数与几何平均数例 1.设 a、bR ,试比较,,,的大小. 解: a、bR+,∴≥2即≤,当且仅当 a=b 时等号成立.又≤= ∴≤当且仅当 a=b 时等号成立. 而≤于是≤≤≤(当且仅当 a=b 时取“=”号).说明:题中的、、、分别叫做正数的调和平均数,几何平均数,算术平均数,平方平均数.也可取特殊值,得出它们的大小关系,然后再证明.变式训练 1:(1)设,已知命题;命题,则是成立的 ( )典型例题基础过关A.必要不充分条件 B.充分不必要条件C.充分必要条件 D.既不充分也不必要条件解:B.解析: 是等号成立的条件(2)若为△ABC 的三条边,且,则( )A. B. C. D.解:D.解析:,又 ∴。(3)设 x > 0, y > 0,, , a 与 b 的大小关系( ) A.a >b B.a a2b3 + a3b2解:证:(a5 + b5 ) (a2b3 + a3b2) = ( a5 a3b2) + (b5 a2b3 ) = a3 (a2 b2 ) b3 (a2 b2) = (a2 b2 ) (a3 b3)= (a + b)(a b)2(a2 + ab + b2) a, b 都是正数,∴a + b, a2 + ab + b2 > 0又 a b,∴(a b)2 > 0 ∴(a + b)(a b)2(a2 + ab + b2) > 0即:a5 + b5 > a2b3 + a3b2变式训练 3:比较下列两个数的大小:(1) (2);(3)从以上两小项的结论中,你否得出更一般的结论?并加以证明解:(1),(2)(3)一般结论:若成立证明 欲证成立只需证也就是 () 从而(*)成立,故 例 4. 甲、乙两地相距 S(千米),汽车从甲地匀速行驶到乙地,速度最大不得超过 c(千米/小时).已知汽车每小时的运输成本(元)由可变部分与固定部分组成.可变部分与速度 v(千米/小时)的平方成正比,且比例系数为正常数 b;固定部分为 a 元.(1) 试将全程运输成本 Y(元)表示成速度 V(千米/小时)的函数.(2) 为使全程运输成本最省,汽车应以多大速度行驶?解: (1) 依题意得,汽车从甲地匀速行驶到乙地所用时间为,全程运输成本为 y=a·+bv2·=s(+bv),故所求函数及其定义域为y=s(+bv)v∈(0,c)(2) s、a、b、v∈R+,故 s(+bv)≥2s 当且仅当=bv 时取等号,此时v=若≤c 即 v=时,全程运输成本最小.若>c,则当 v∈(0,c)时,y=s(+...