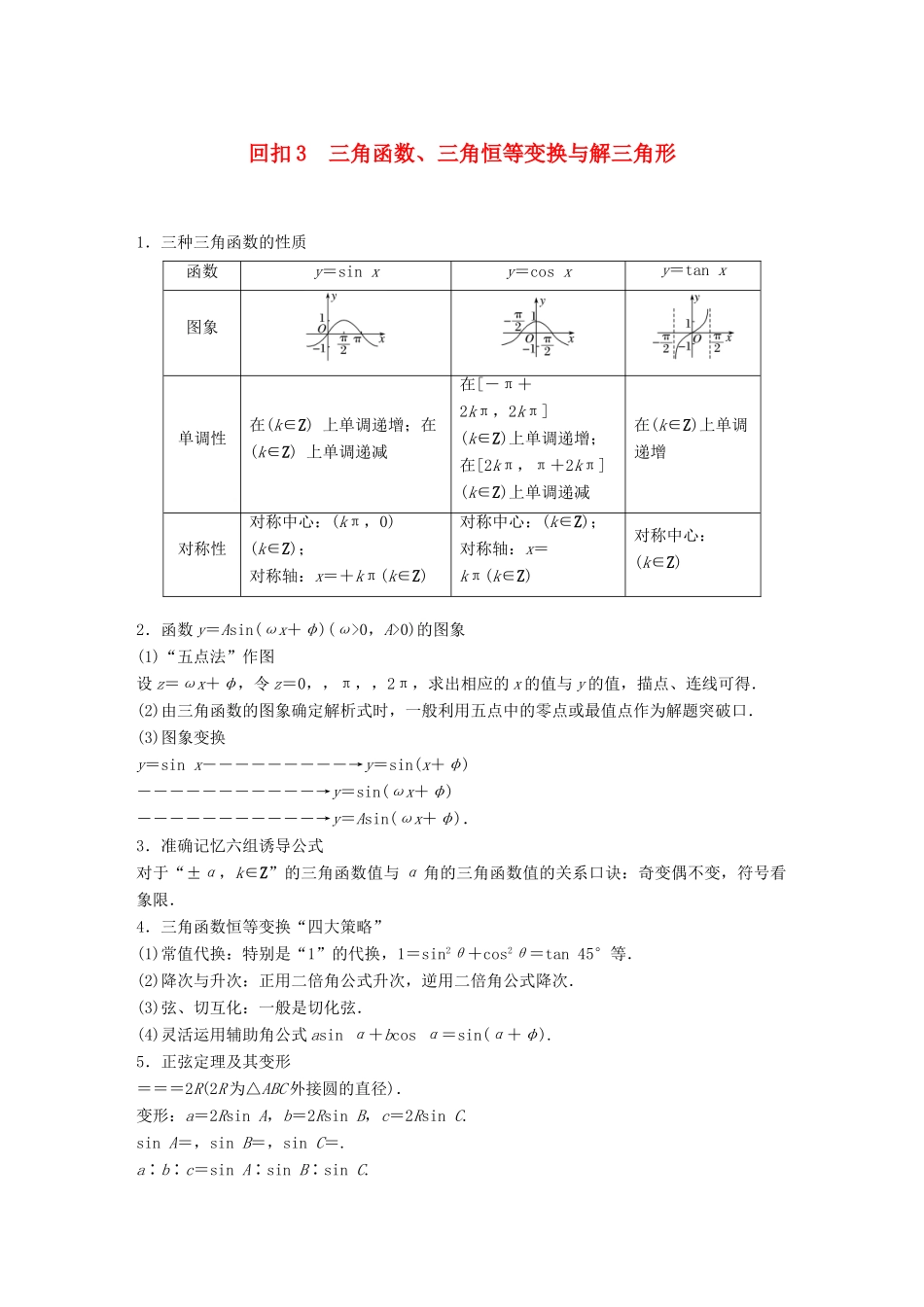
回扣 3 三角函数、三角恒等变换与解三角形1.三种三角函数的性质函数y=sin xy=cos xy=tan x图象单调性在(k∈Z) 上单调递增;在(k∈Z) 上单调递减在[-π+2kπ,2kπ](k∈Z)上单调递增;在[2kπ,π+2kπ](k∈Z)上单调递减在(k∈Z)上单调递增对称性对称中心:(kπ,0)(k∈Z);对称轴:x=+kπ(k∈Z)对称中心:(k∈Z);对称轴:x=kπ(k∈Z)对称中心:(k∈Z)2.函数 y=Asin(ωx+φ)(ω>0,A>0)的图象(1)“五点法”作图设 z=ωx+φ,令 z=0,,π,,2π,求出相应的 x 的值与 y 的值,描点、连线可得.(2)由三角函数的图象确定解析式时,一般利用五点中的零点或最值点作为解题突破口.(3)图象变换y=sin x―――――――――→y=sin(x+φ)―――――――――――→y=sin(ωx+φ)―――――――――――→y=Asin(ωx+φ).3.准确记忆六组诱导公式对于“±α,k∈Z”的三角函数值与 α 角的三角函数值的关系口诀:奇变偶不变,符号看象限.4.三角函数恒等变换“四大策略”(1)常值代换:特别是“1”的代换,1=sin2θ+cos2θ=tan 45°等.(2)降次与升次:正用二倍角公式升次,逆用二倍角公式降次.(3)弦、切互化:一般是切化弦.(4)灵活运用辅助角公式 asin α+bcos α=sin(α+φ).5.正弦定理及其变形===2R(2R 为△ABC 外接圆的直径).变形:a=2Rsin A,b=2Rsin B,c=2Rsin C.sin A=,sin B=,sin C=.a∶b∶c=sin A∶sin B∶sin C.6.余弦定理及其推论、变形a2=b2+c2-2bccos A,b2=a2+c2-2accos B,c2=a2+b2-2abcos C.推论:cos A=,cos B=,cos C=.变形:b2+c2-a2=2bccos A,a2+c2-b2=2accos B,a2+b2-c2=2abcos C.7.面积公式S△ABC=bcsin A=acsin B=absin C.1.利用同角三角函数的平方关系式求值时,不要忽视角的范围,要先判断函数值的符号.2.在求三角函数的值域(或最值)时,不要忽略 x 的取值范围.3.求函数 f(x)=Asin(ωx+φ)的单调区间时,要注意 A 与 ω 的符号,当 ω<0 时,需把ω 的符号化为正值后求解.4.三角函数图象变换中,注意由 y=sin ωx 的图象变换得到 y=sin(ωx+φ)的图象时,平移量为,而不是 φ.5.在已知两边和其中一边的对角利用正弦定理求解时,要注意检验解是否满足“大边对大角”,避免增解.1.若 sin θ·cos θ=,则 tan θ+的值是( )A.-2 B.2 C.±2 D.答案 B解析 t...