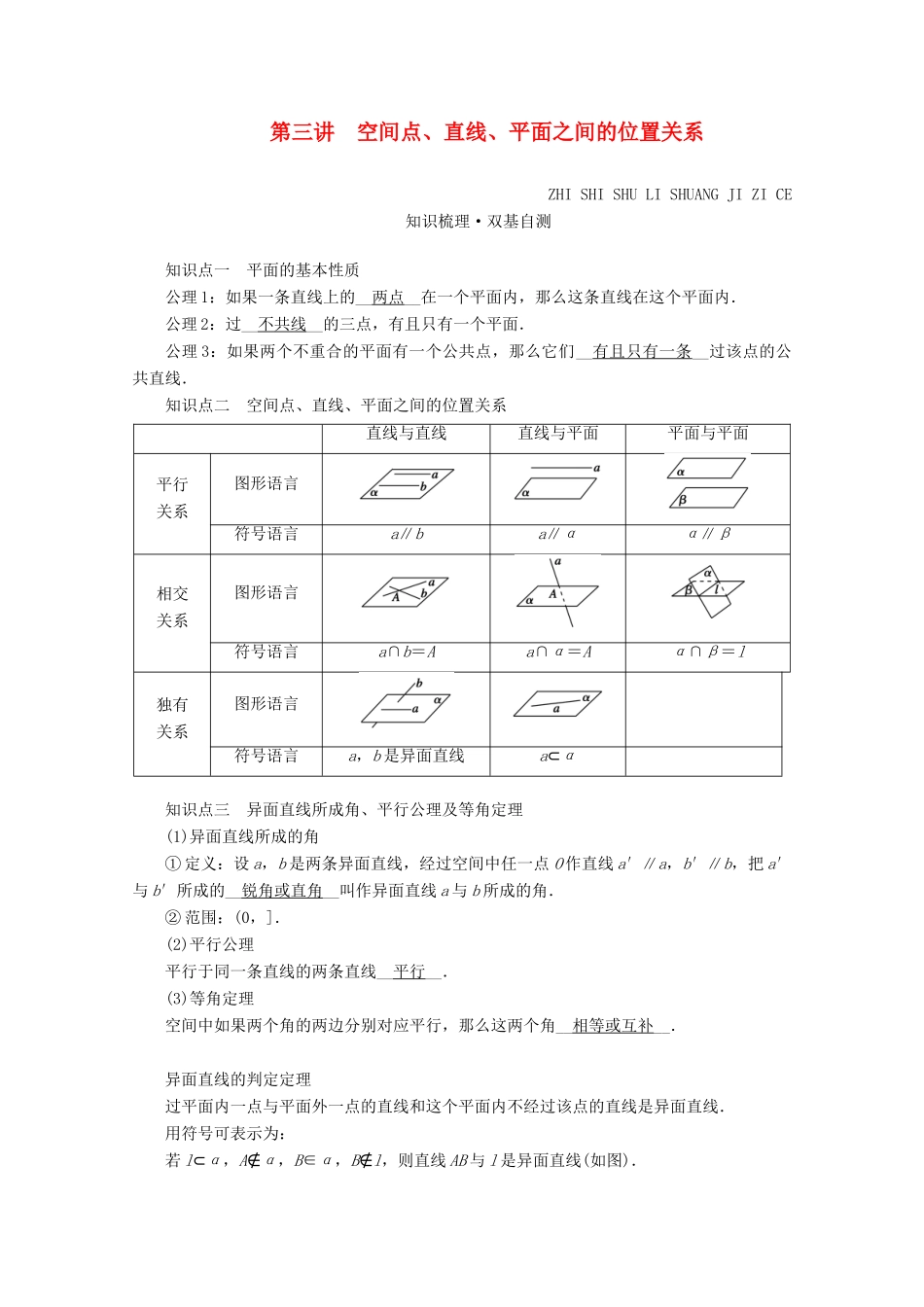
第三讲 空间点、直线、平面之间的位置关系ZHI SHI SHU LI SHUANG JI ZI CE知识梳理·双基自测 知识点一 平面的基本性质公理 1:如果一条直线上的__两点__在一个平面内,那么这条直线在这个平面内.公理 2:过__不共线__的三点,有且只有一个平面.公理 3:如果两个不重合的平面有一个公共点,那么它们__有且只有一条__过该点的公共直线.知识点二 空间点、直线、平面之间的位置关系直线与直线直线与平面平面与平面平行关系图形语言符号语言a∥ba∥αα∥β相交关系图形语言符号语言a∩b=Aa∩α=Aα∩β=l独有关系图形语言符号语言a,b 是异面直线a⊂α知识点三 异面直线所成角、平行公理及等角定理(1)异面直线所成的角① 定义:设 a,b 是两条异面直线,经过空间中任一点 O 作直线 a′∥a,b′∥b,把 a′与 b′所成的__锐角或直角__叫作异面直线 a 与 b 所成的角.② 范围:(0,].(2)平行公理平行于同一条直线的两条直线__平行__.(3)等角定理空间中如果两个角的两边分别对应平行,那么这两个角__相等或互补__.异面直线的判定定理过平面内一点与平面外一点的直线和这个平面内不经过该点的直线是异面直线.用符号可表示为:若 l⊂α,A∉α,B∈α,B∉l,则直线 AB 与 l 是异面直线(如图).题组一 走出误区1.(多选题)下列结论正确的是( AC )A.如果两个不重合的平面 α,β 有一条公共直线 a,就说平面 α,β 相交,并记作α∩β=aB.如果两个平面有三个公共点,则这两个平面重合C.经过两条相交直线,有且只有一个平面D.两两相交的三条直线共面题组二 走进教材2.(必修 2P52B 组 T1)如图所示,在正方体 ABCD-A1B1C1D1中,E,F 分别是 AB,AD 的中点,则异面直线 B1C 与 EF 所成角的大小为( C )A.30° B.45° C.60° D.90°[解析] 解法一:因为 CD∥AB,所以∠BAE(或其补角)即为异面直线 AE 与 CD 所成的角设正方体的棱长为 2,则 BE=.因为 AB⊥平面 BB1C1C,所以 AB⊥BE.在 Rt△ABE 中,tan∠BAE==,故选 C.解 法 二 : 连 接 B1D1 , D1C , 则 B1D1∥EF , 故 ∠ D1B1C 即 为 所 求 的 角 . 又 B1D1 = B1C =D1C,∴△B1D1C 为等边三角形,∴∠D1B1C=60°.故选 C.3.(必修 2P45例 2)如图,在三棱锥 A-BCD 中,E,F,G,H 分别是棱 AB,BC,CD,DA 上的点, (1)若=且=,则 E、F、G、H 是否共面.__...