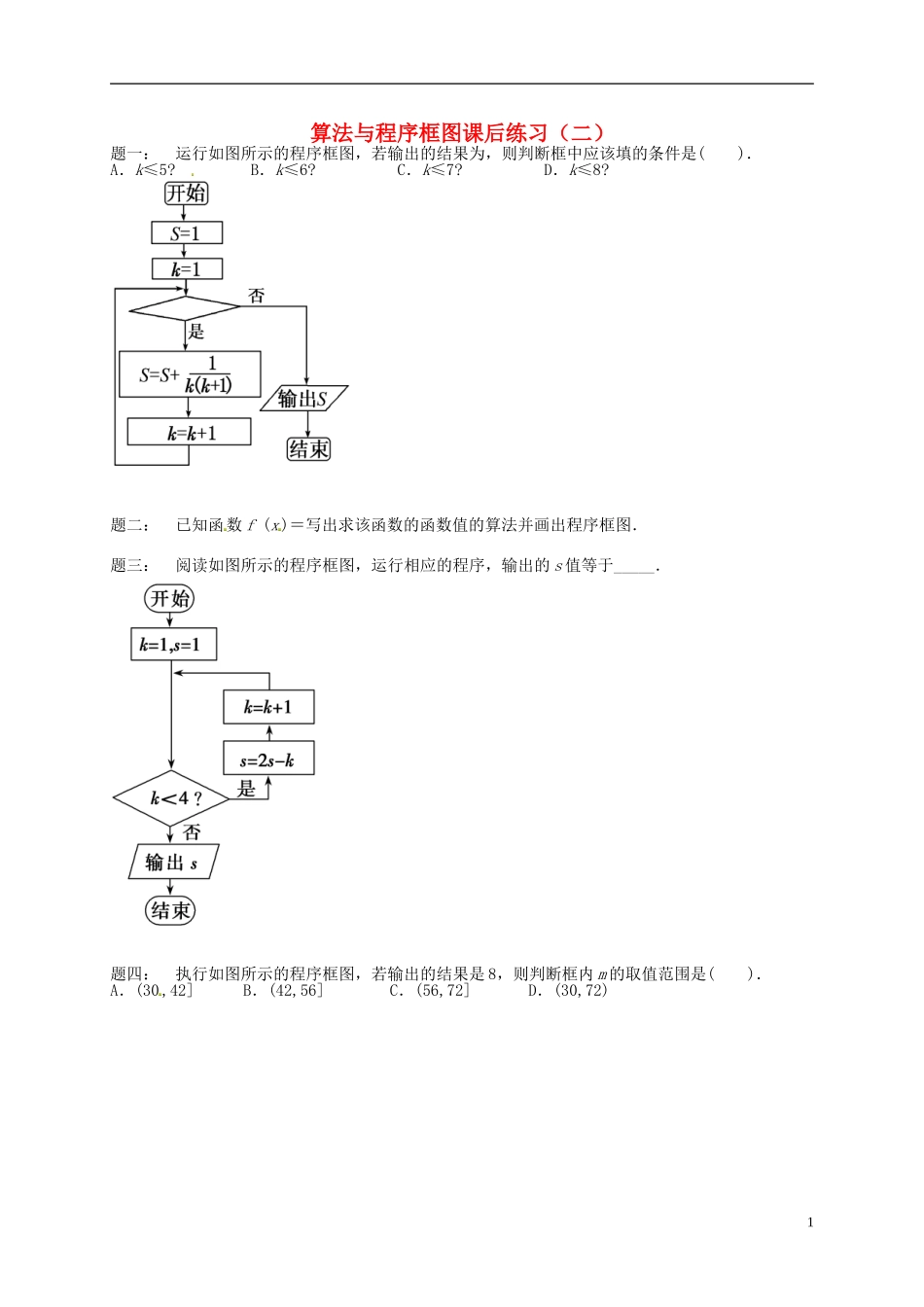
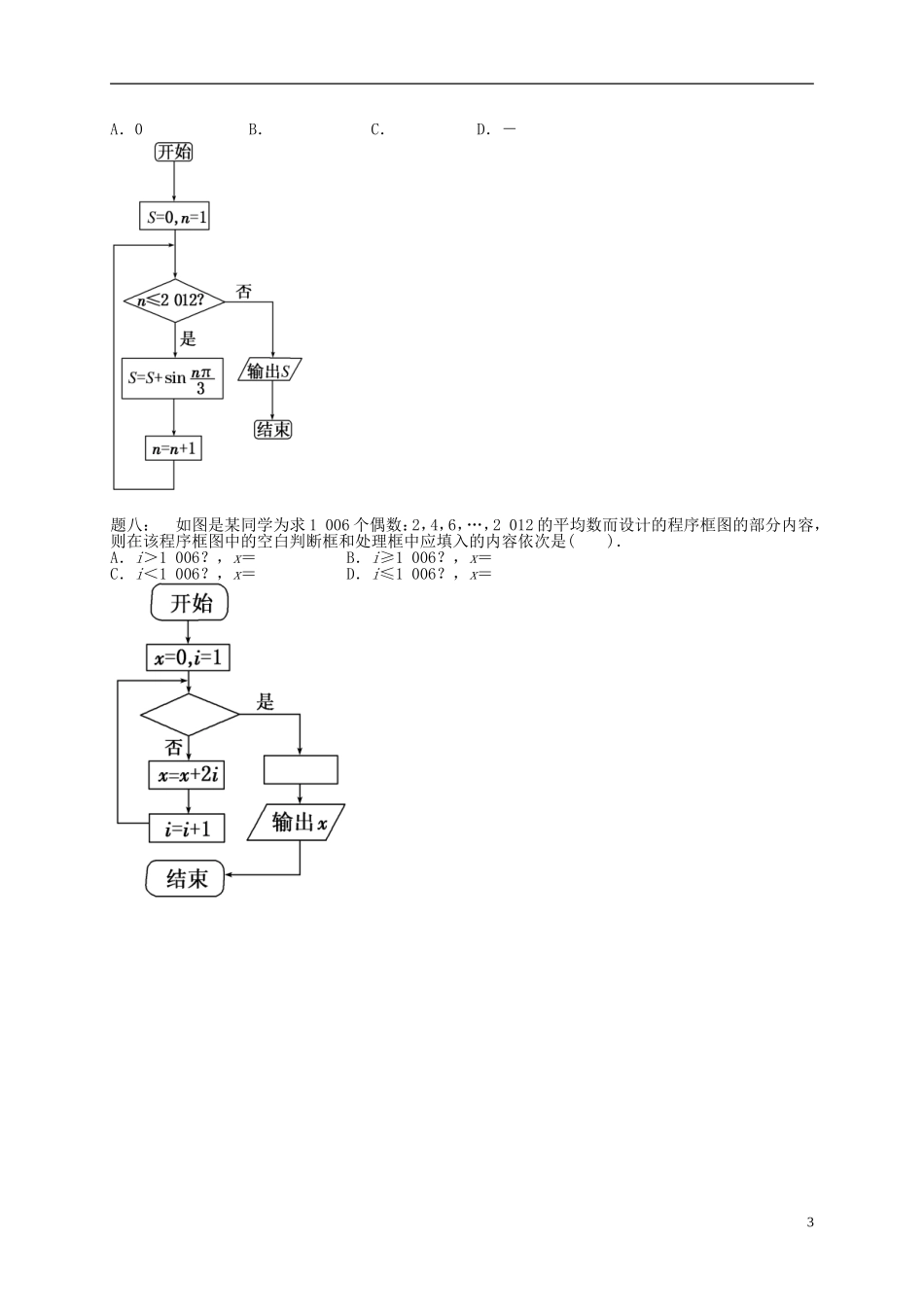
算法与程序框图课后练习(二)题一:运行如图所示的程序框图,若输出的结果为,则判断框中应该填的条件是( ).A.k≤5? B.k≤6? C.k≤7? D.k≤8?题二:已知函数 f (x )=写出求该函数的函数值的算法并画出程序框图.题三:阅读如图所示的程序框图,运行相应的程序,输出的 s 值等于_____.题四:执行如图所示的程序框图,若输出的结果是 8,则判断框内 m 的取值范围是( ).A.(30 ,42] B.(42,56] C.(56,72] D.(30,72)1题五:执行如图所示的程序框图,若输出的 n=5,则输入整数 P 的最小值是( ).A.7 B.8 C.15 D.16题六:若某程序框图如图所示 , 则输出的 p 的值是( ).A.21 B.286 C.30 D.55题七:阅读如图所示的程序框图,输出的结果 S 的值为( )2A.0 B. C. D.- 题八:如图是某同学为求 1 006 个偶数:2,4,6,…,2 012 的平均数而设计的程序框图的部分内容,则在该程序框图中的空白判断框和处理框中应填入的内容依次是( ).A.i>1 006?,x= B.i≥1 006?,x=C.i<1 006?,x= D.i≤1 006?,x=3算法与程序框图课后练习参考答案题一: B.详解:第一次运行 S=1+,k=2;第二次运行 S=1++,k=3;…;第 n 次运行 S=1+++…+=,k=n+1,此时结束循环,得 n=6,故判断框中应该填入“k≤6?”.题二: 如图.详解:算法如下:第一步,输入 x.第二步,如果 x<0,那么使 f (x)=3x-1.否则 f (x)=2-5x.第三步,输出函数值 f(x).程序框图如下:题三: -3.详解:逐次循环可得 s 的值,注意循环结束的条件.第一次循环:s= 1,k=1<4,s=2×1-1=1,k=1+1=2;第二次循环:k=2<4,s=2×1-2=0,k=2+1=3;第三次循环:k=3<4,s=2×0-3=-3,k=3+1=4;当 k=4 时,k<4 不成立,循环结束,此时 s=-3.题四: B.详解:由题知,k=1,S=0,第一次循环,S=2,k=2;第二次循环,S=2+2×2=6,k=3;…;第六次循环,S=30+2×6=42,k=6+1=7;第七次循环,S=42+2×7=56,k=7+1=8,此时应输出 k 的值,从而易知 m 的取值范围是(42,56].4题五: B.详解:依题意得,当输出的 n=5 时,数列{2 n 1 }的前 4 项和开始不 小于整数 P,注意到数列{2n1 }的前 3项和等于 1+2+4=7,因此输入整数 P 的最小值是 8.题六: C.详解:依题意,注意到 1+22+32=14<20<1...