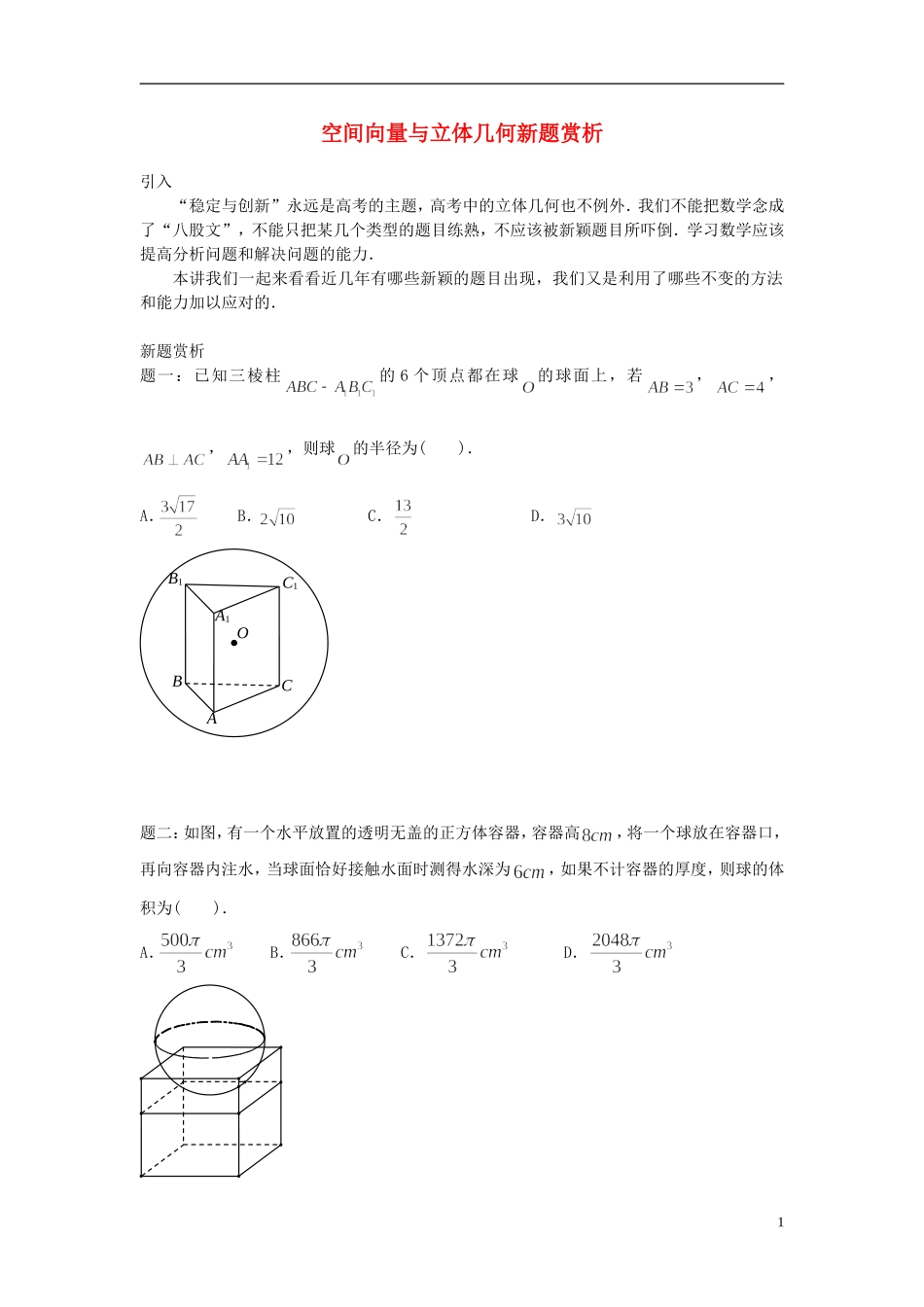
空间向量与立体几何新题赏析引入“稳定与创新”永远是高考的主题,高考中的立体几何也不例外.我们不能把数学念成了“八股文”,不能只把某几个类型的题目练熟,不应该被新颖题目所吓倒.学习数学应该提高分析问题和解决问题的能力.本讲我们一起来看看近几年有哪些新颖的题目出现,我们又是利用了哪些不变的方法和能力加以应对的.新题赏析题一:已知三棱柱的 6 个顶点都在球的球面上,若,,,,则球的半径为( ).A.B.C.D.题二:如图,有一个水平放置的透明无盖的正方体容器,容器高,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为,如果不计容器的厚度,则球的体积为( ).A.B.C.D.OABCA1B1C11题三:如图,正方体的棱长为 1,为的中点,为线段上的动点,过点的平面截该正方体所得的截面记为 S ,则下列命题正确的是 (写出所有正确命题的编号).① 当时, S 为四边形;②当12CQ 时, S 为等腰梯形;③ 当34CQ 时, S 与11C D 的交点 R 满足113C R ;④当 314CQ时, S 为六边形;⑤ 当1CQ 时, S 的面积为62.题四:如图,圆锥顶点为 P ,底面圆心为O ,其母线与底面所成的角为 22.5 .AB 和CD 是底面圆O 上的两条平行的弦,轴OP 与平面 PCD 所成的角为60 .(Ⅰ)证明:平面 PAB 与平面 PCD 的交线平行于底面;(Ⅱ)求cosCOD.题五:如图,在四棱柱中,侧棱,,PCBDAC1B1D1A1QPBAOCD2,,,,.(Ⅰ)求证:;(Ⅱ)若直线与平面所成角的正弦值为,求的值;(Ⅲ)现将与四棱柱形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱柱形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新四棱柱中,记其中最小的表面积为,写出的表达式(直接写出答案,不必要说明理由).学习提醒平时全面备考,考时熟题不错、新题不慌!新题赏析题一:C 题二:A 题三:①②③⑤ 题四:(Ⅰ)略;(Ⅱ)题五:(Ⅰ)略;(Ⅱ)1;(Ⅲ)ABCDEA1B1C1D13