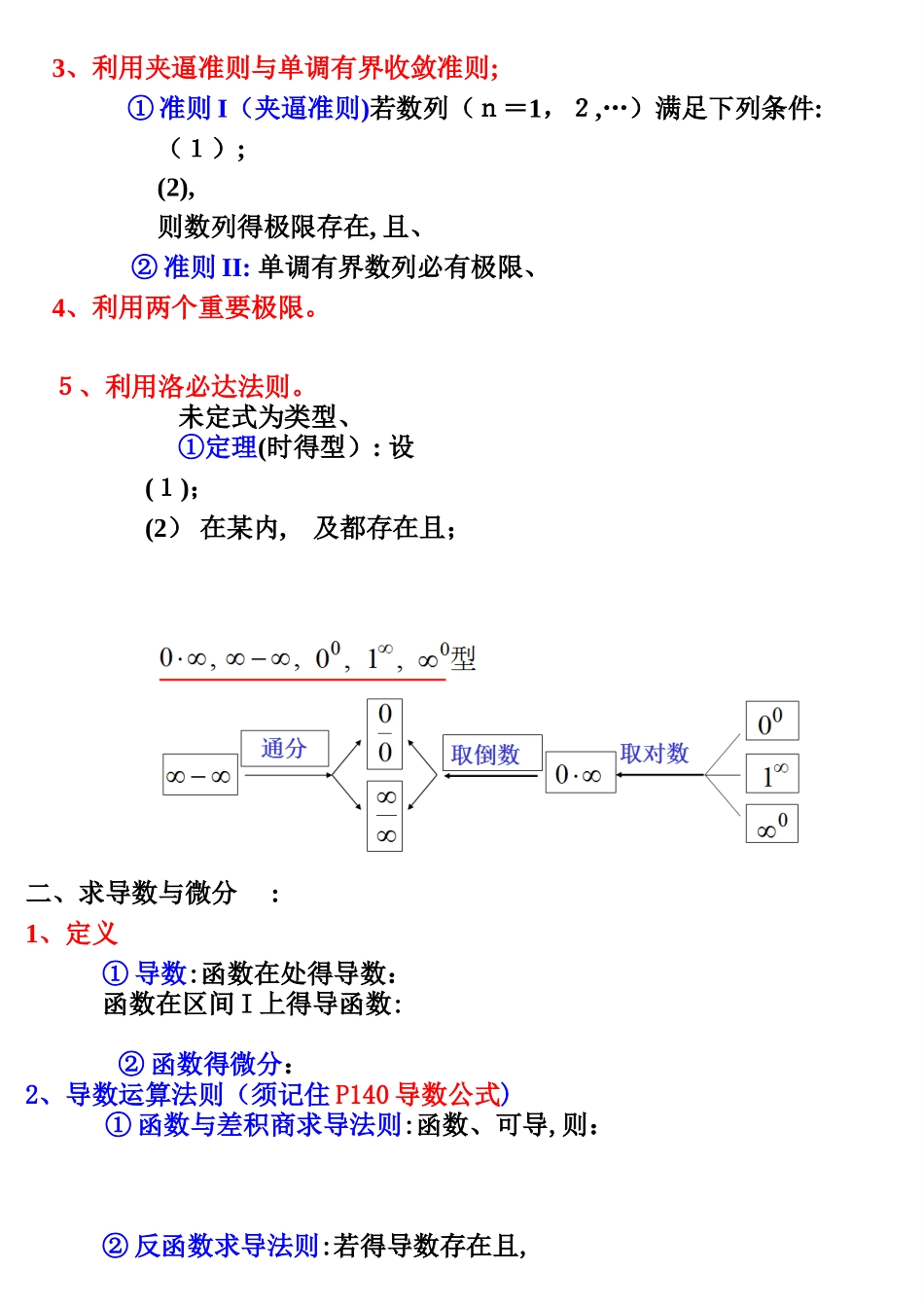
高数总复习(上)一、求极限得方法:1、利用运算法则与基本初等函数得极限;①、定理 若, 则(加减运算) (乘法运算) (除法运算) 推论1: (为正整数) 推论 2: ② 结论 1:结论 2: 就是基本初等函数,其定义区间为 D,若,则 2、利用等价无穷小代换及无穷小得性质;① 定义 1: 若或()则称就是当 (或)时得无穷小、 定义 2: 就是自变量在同一变化过程中得无穷小: 若, 则称与就是等价无穷小, 记为、 ② 性质 1:有限个无穷小得与也就是无穷小、性质 2: 有界函数与无穷小得乘积就是无穷小、推论 1: 常数与无穷小得乘积就是无穷小、推论 2: 有限个无穷小得乘积也就是无穷小、定理2(等价无穷小替换定理) 设, 且存在, 则、 (因式替换原则)常用等价无穷小: 3、利用夹逼准则与单调有界收敛准则;① 准则 I(夹逼准则)若数列(n=1,2,…)满足下列条件: (1);(2),则数列得极限存在, 且、② 准则 II: 单调有界数列必有极限、4、利用两个重要极限。 5、利用洛必达法则。 未定式为类型、 ①定理(时得型): 设(1);(2) 在某内, 及都存在且; 二、求导数与微分 :1、定义① 导数:函数在处得导数:函数在区间 I 上得导函数:② 函数得微分:2、导数运算法则(须记住 P140 导数公式)① 函数与差积商求导法则:函数、可导,则:② 反函数求导法则:若得导数存在且,则反函数得导数也存在且为 ③ 复合函数求导法则(链式法则):可导,可导,则可导,且④ 隐函数求导法则: ⑤ 参数方程求导法则: 若则、3、微分运算法则三、求积分: 1、概念:原函数、不定积分。定积分就是一个数,就是一个与得极限形式。性质1:性质 2: 性质 3:性质 4: (去绝对值, 分段函数积分)性质 5:2、计算公式: P18 6基本积分表; P 2 03 常用积分公式;① 第一换元法(凑微分): ② 第二换元法: ③分部积分法:④ 有理函数积分:混合法 (赋值法+特别值法)确定系数循环解出; 递推公式分部化简 ;⑤ 牛顿莱布尼茨公式:⑥ 定积分换元法: (换元换限,配元(凑微)不换限) ⑦ 定积分分部积分法:⑧ 结论(偶倍奇零):① 若函数为偶函数,则。② 若函数为奇函数,则 注意:1、 利用“偶倍奇零”简化定积分得计算;2、 定积分几何意义求一些特别得积分(如) ⑨ 变限积分求导四、微分与积分得应用1. 推断函数得单调性、凹凸性、求其极值、拐点、描绘函数图形① 推断单调性:第一步:找使 得点与不可导...