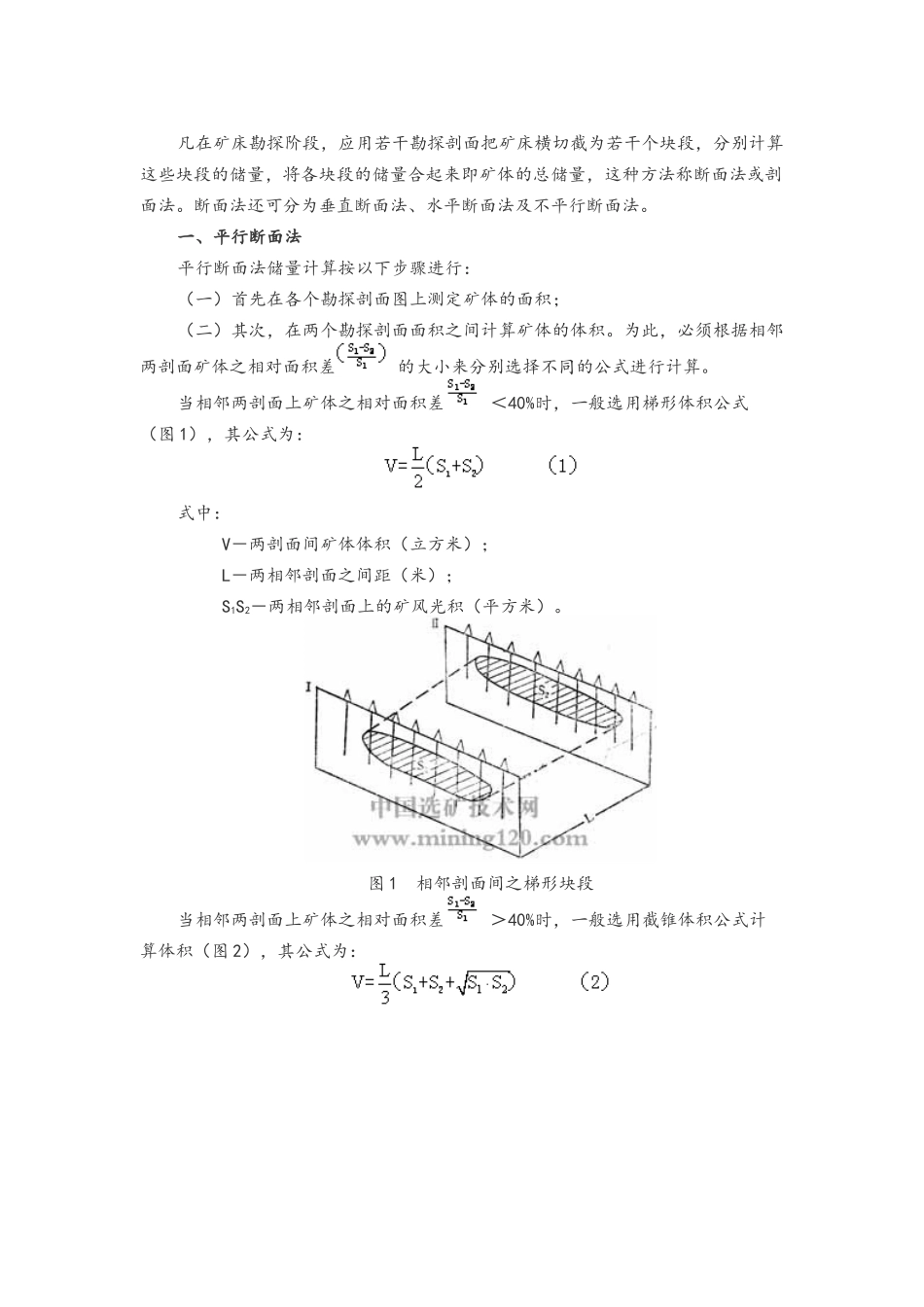
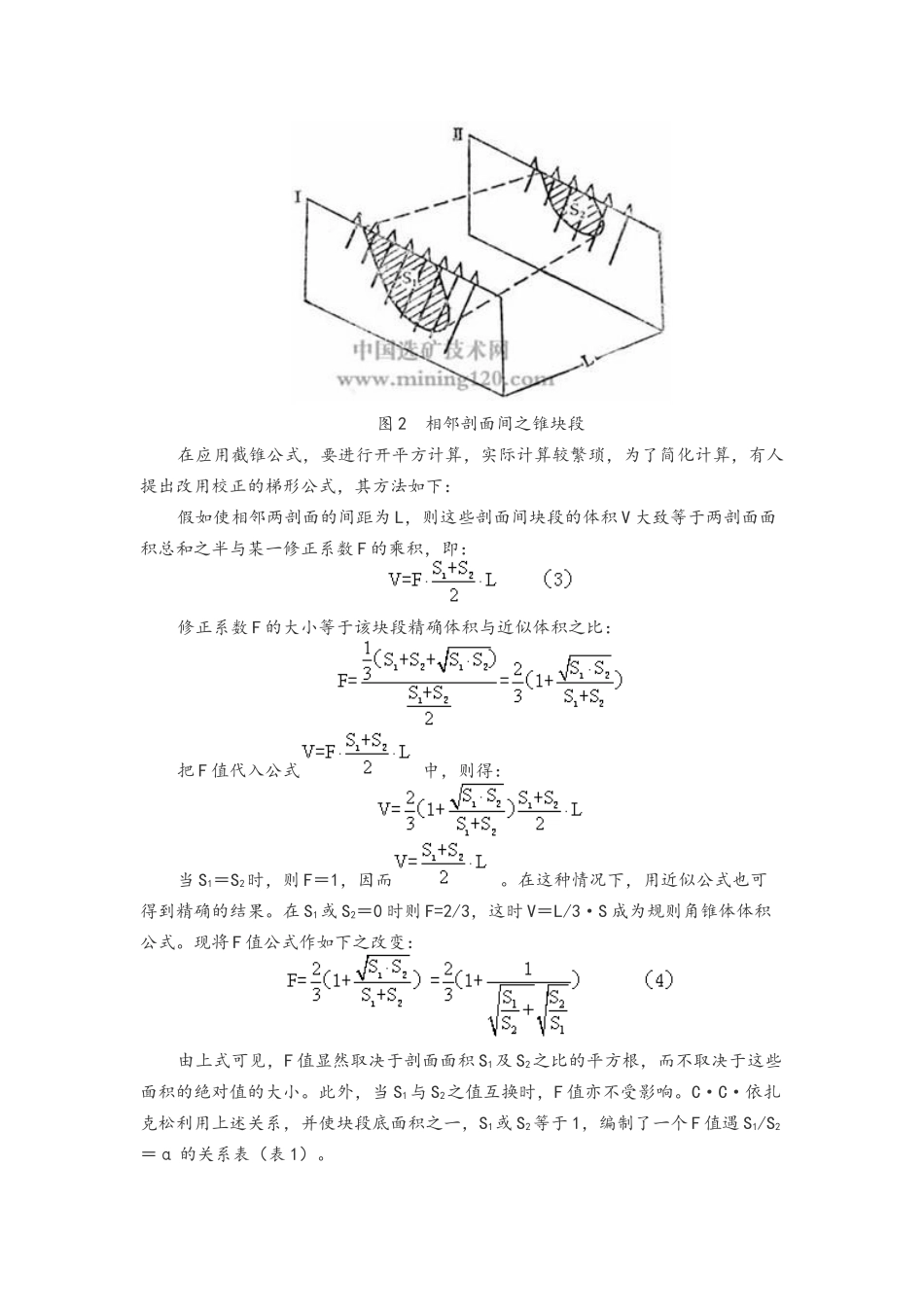
凡在矿床勘探阶段,应用若干勘探剖面把矿床横切截为若干个块段,分别计算这些块段的储量,将各块段的储量合起来即矿体的总储量,这种方法称断面法或剖面法。断面法还可分为垂直断面法、水平断面法及不平行断面法。一、平行断面法平行断面法储量计算按以下步骤进行:(一)首先在各个勘探剖面图上测定矿体的面积;(二)其次,在两个勘探剖面面积之间计算矿体的体积。为此,必须根据相邻两剖面矿体之相对面积差 的大小来分别选择不同的公式进行计算。当相邻两剖面上矿体之相对面积差 <40%时,一般选用梯形体积公式(图 1),其公式为:式中: V-两剖面间矿体体积(立方米); L-两相邻剖面之间距(米); S1S2-两相邻剖面上的矿风光积(平方米)。图 1 相邻剖面间之梯形块段当相邻两剖面上矿体之相对面积差 >40%时,一般选用截锥体积公式计算体积(图 2),其公式为:图 2 相邻剖面间之锥块段在应用截锥公式,要进行开平方计算,实际计算较繁琐,为了简化计算,有人提出改用校正的梯形公式,其方法如下:假如使相邻两剖面的间距为 L,则这些剖面间块段的体积 V 大致等于两剖面面积总和之半与某一修正系数 F 的乘积,即:修正系数 F 的大小等于该块段精确体积与近似体积之比:把 F 值代入公式 中,则得:当 S1=S2时,则 F=1,因而 。在这种情况下,用近似公式也可得到精确的结果。在 S1或 S2=0 时则 F=2/3,这时 V=L/3·S 成为规则角锥体体积公式。现将 F 值公式作如下之改变:由上式可见,F 值显然取决于剖面面积 S1及 S2之比的平方根,而不取决于这些面积的绝对值的大小。此外,当 S1与 S2之值互换时,F 值亦不受影响。C·C·依扎克松利用上述关系,并使块段底面积之一,S1或 S2等于 1,编制了一个 F 值遇 S1/S2=α 的关系表(表 1)。表 1 α<1α>1F 值α<1α>1F 值0.710.500.330.250.200.170.100.080.070.060.050.040.031.42.03.04.05.06.010.012.014.016.020.025.030.00.9950.9800.9550.9330.9150.9000.8590.8450.8330.8240.8090.7950.7850.0250.0200.0170.0140.0100.0070.0050.0030.0020.0020.0010.00140.050.060.070.0100.0140.0200.0300.0400.0500.0700.01000.00.7700.7600.7510.7450.7330.7240.7140.7060.7000.6960.6920.689 表 1 表明,当 S1与 S2之比值 α 在 0.71~1.4 以内时,F 值可略而不计,因为误差小于 1%,尚未超出储量计算的一般精度范围。按表 1...