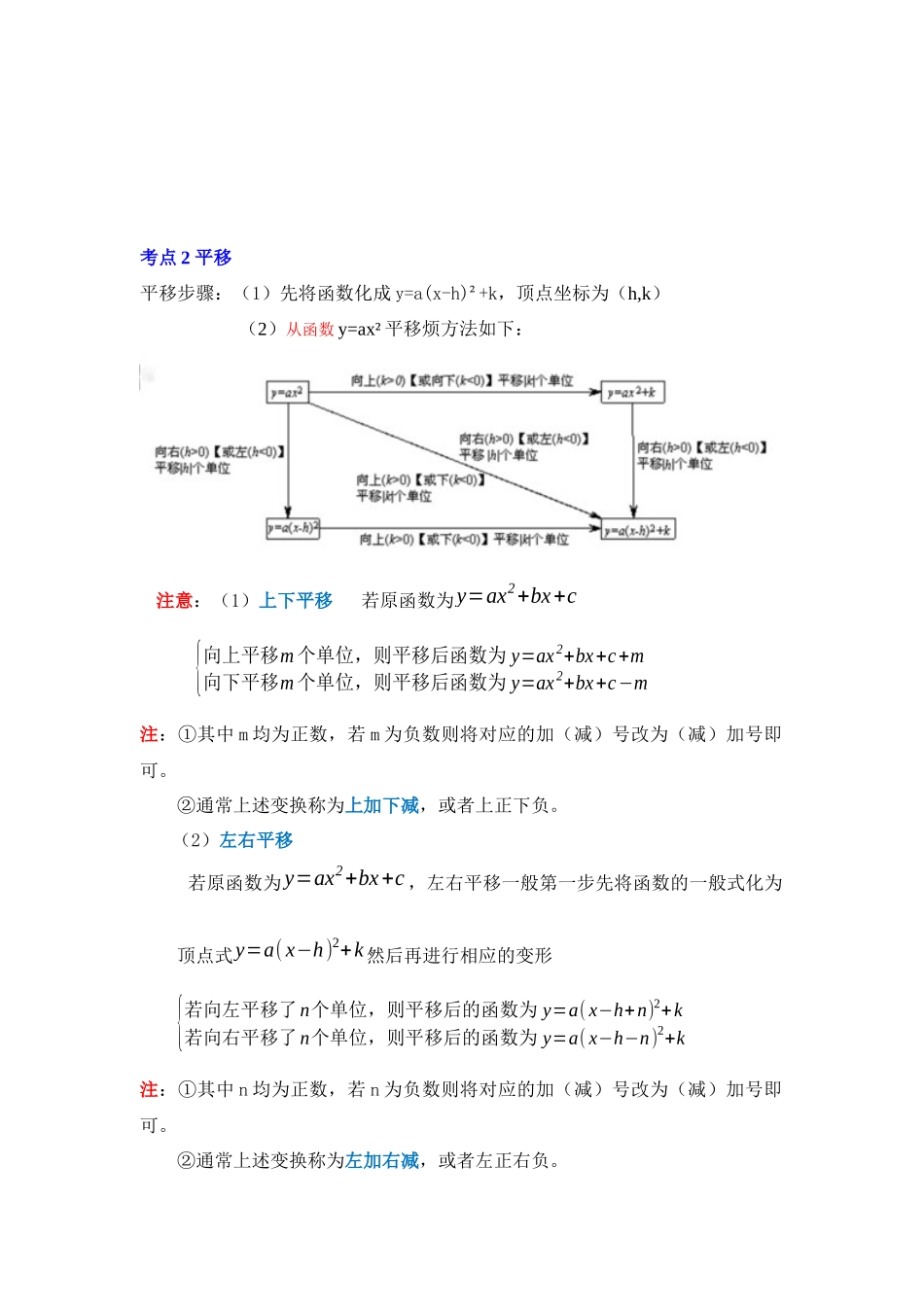
专题 22.1.4 二次函数 y=a(x-h)²+k(a≠0)图像和性质(知识解读)【直击考点】【学习目标】1. 会用描点法画出二次函数 y=a(x-h)²+k(a、h、k 是常数,a≠0)的图像,并熟练掌握 y=a(x-h)²+k 图像有性质,并能用函数掌握二次函数 y=a(x-h)²+k 的性质解决一些实际问题;2. 掌握 y=a(x-h)²+k 与 y=ax² 之间的关系。【知识点梳理】考点 1 y=a(x-h)²+k(a≠0)与 y=a(x-h)²(a≠0)的图像与性质考点 2 平移平移步骤:(1)先将函数化成 y=a(x-h)²+k,顶点坐标为(h,k)(2)从函数 y=ax² 平移烦方法如下:注意:(1)上下平移 若原函数为y=ax2+bx+c {向上平移m个单位,则平移后函数为 y=ax 2+bx+c+m向下平移m个单位,则平移后函数为 y=ax 2+bx+c−m注:①其中 m 均为正数,若 m 为负数则将对应的加(减)号改为(减)加号即可。②通常上述变换称为上加下减,或者上正下负。(2)左右平移 若原函数为y=ax2+bx+c ,左右平移一般第一步先将函数的一般式化为顶点式y=a( x−h)2+k 然后再进行相应的变形{若向左平移了n个单位,则平移后的函数为 y=a( x−h+n)2+k若向右平移了n个单位,则平移后的函数为 y=a( x−h−n)2+k注:①其中 n 均为正数,若 n 为负数则将对应的加(减)号改为(减)加号即可。②通常上述变换称为左加右减,或者左正右负。【典例分析】【考点 1 y=a(x-h)²+k(a≠0)的图像和性质】【例 1】(2025 九下·南雄)抛物线 y=(x1﹣ )22﹣ 的顶点坐标为( )A.(1,2)B.(1,﹣2)C.(﹣1,2) D.(﹣1,﹣2)【变式 1-1】(2024 九上·海曙期末)已知抛物线 y=2(x−3)2−5 , 其对称轴是( )A.直线 x=−3B.直线 x=3 C.直线 x=−5 D.直线 x=5【变式 1-2】(2024 九上·肃州期末)抛物线 y=− 12 (x −2)2+5 的顶点坐标是 .【变式 1-3】(2024 九上·昌平期末)关于二次函数 y=-(x -2)2+3,以下说法正确的是( )A.当 x>-2 时,y 随 x 增大而减小B.当 x>-2 时,y 随 x 增大而增大C.当 x>2 时,y 随 x 增大而减小D.当 x>2 时,y 随 x 增大而增大【例 2】(2024 九上·武汉月考)已知二次函数 y=﹣4(x1﹣ )2+k 的图象上有三点 A( ❑√2 ,y1),B(﹣2,y2),C(5,y3),则 y1、y2、y3的大小关系为( ) A.y1>y2>y3 B.y2>y1>y3 C.y3>y1>y2 D.y3>y2>y1【变式 2-1】(202...