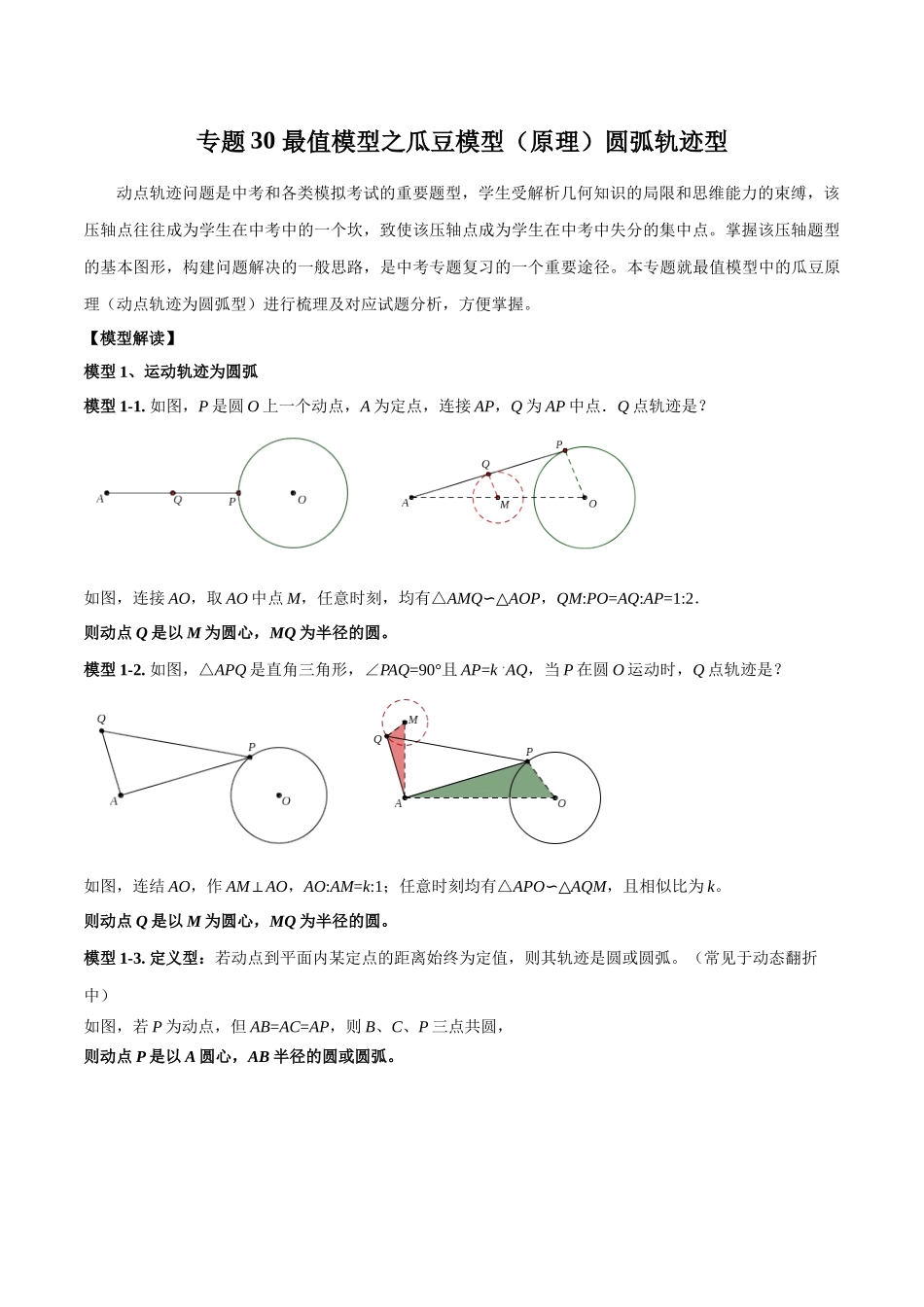
专题 30 最值模型之瓜豆模型(原理)圆弧轨迹型动点轨迹问题是中考和各类模拟考试的重要题型,学生受解析几何知识的局限和思维能力的束缚,该压轴点往往成为学生在中考中的一个坎,致使该压轴点成为学生在中考中失分的集中点。掌握该压轴题型的基本图形,构建问题解决的一般思路,是中考专题复习的一个重要途径。本专题就最值模型中的瓜豆原理(动点轨迹为圆弧型)进行梳理及对应试题分析,方便掌握。【模型解读】模型 1、运动轨迹为圆弧模型 1-1. 如图,P 是圆 O 上一个动点,A 为定点,连接 AP,Q 为 AP 中点.Q 点轨迹是? 如图,连接 AO,取 AO 中点 M,任意时刻,均有△AMQ∽△AOP,QM:PO=AQ:AP=1:2.则动点 Q 是以 M 为圆心,MQ 为半径的圆。模型 1-2. 如图,△APQ 是直角三角形,∠PAQ=90°且 AP=k AQ,当 P 在圆 O 运动时,Q 点轨迹是? 如图,连结 AO,作 AM⊥AO,AO:AM=k:1;任意时刻均有△APO∽△AQM,且相似比为 k。则动点 Q 是以 M 为圆心,MQ 为半径的圆。模型 1-3. 定义型:若动点到平面内某定点的距离始终为定值,则其轨迹是圆或圆弧。(常见于动态翻折中)如图,若 P 为动点,但 AB=AC=AP,则 B、C、P 三点共圆,则动点 P 是以 A 圆心,AB 半径的圆或圆弧。 模型 1-4. 定边对定角(或直角)模型1)一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧.如图,若 P 为动点,AB 为定值,∠APB=90°,则动点 P 是以 AB 为直径的圆或圆弧。2)一条定边所对的角始终为定角,则定角顶点轨迹是圆弧.如图,若 P 为动点,AB 为定值,∠APB 为定值,则动点 P 的轨迹为圆弧。PPABOP PPABP【模型原理】动点的轨迹为定圆时,可利用:“一定点与圆上的动点距离最大值为定点到圆心的距离与半径之和,最小值为定点到圆心的距离与半径之差”的性质求解。例 1.(2025·山东泰安·统考中考真题)如图,在平面直角坐标系中,的一条直角边在 x 轴上,点 A 的坐标为;中,,连接,点 M 是中点,连接.将以点 O 为旋转中心按顺时针方向旋转,在旋转过程中,线段的最小值是( ) A.3B.C.D.2例 2.(2025·四川广元·统考一模)如图,线段为的直径,点在的延长线上,,,点是上一动点,连接,以为斜边在的上方作 Rt,且使,连接,则长的最大值为 .例 3.(2025·四川宜宾·统考中考真题)如图,是正方形边的中点,是正方形内一点,连接,...