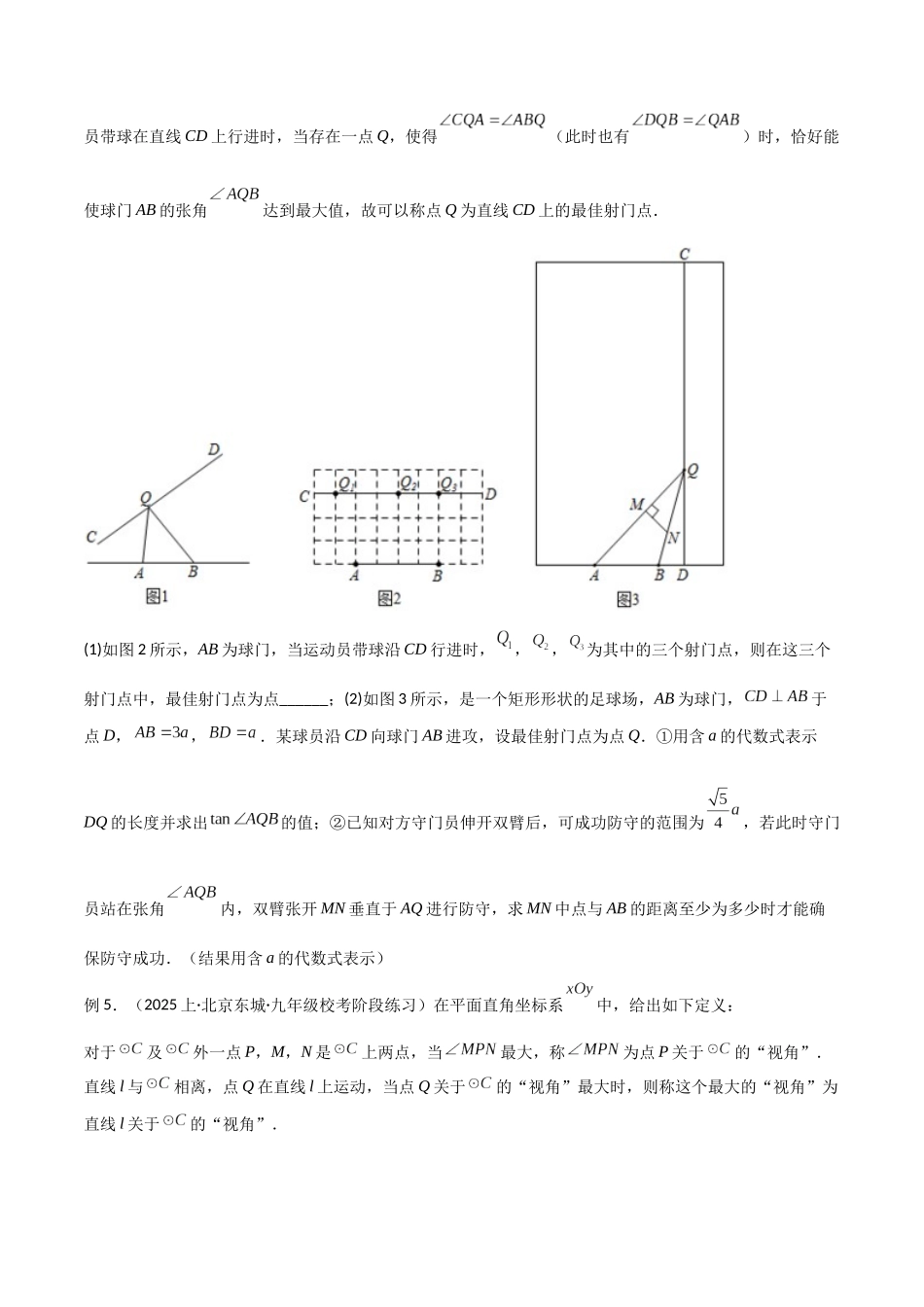
专题 35 圆中的重要模型之定角定高模型、米勒最大角模型圆在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就圆形中的重要模型(米勒最大视角(张角)模型、定角定高(探照灯)模型)进行梳理及对应试题分析,方便掌握。近几年一些中考几何问题涉及了“最大视角”与“定角定高”模型,问题往往以动点为背景,与最值相结合,综合性较强,解析难度较大,学生难以找到问题的切入点,不能合理构造辅助圆来求解。实际上,这样的问题中隐含了几何的“最大视角”与“定角定高”模型,需要对其中的动点轨迹加以剖析,借助圆的特性来探究最值情形。而轨迹问题是近些年中考压轴题的热点和难点,既可以与最值结合考查,也可以与轨迹长结合考查,综合性较强、难度较大。模型 1.米勒最大张角(视角)模型【模型解读】已知点 A,B 是∠MON 的边 ON 上的两个定点,点 C 是边 OM 上的动点,则当 C 在何处时,∠ACB 最大?对米勒问题在初中最值的考察过程中,也成为最大张角或最大视角问题。米勒定理:已知点 AB 是∠MON 的边 ON 上的两个定点,点 C 是边 OM 上的一动点,则当且仅当三角形ABC 的外圆与边 OM 相切于点 C 时,∠ACB 最大。MONABC BAONMC【模型证明】如图 1,设 C’是边 OM 上不同于点 C 的任意一点,连结 A,B,因为∠AC’B 是圆外角,∠ACB 是圆周角,易证∠AC’B 小于∠ACB,故∠ACB 最大。DBAONMCC'在三角形 AC’D 中, 又 【解题关键】常常以解析几何、平面几何和实际应用为背景进行考查。若能从题设中挖出隐含其中的米勒问题模型,并能直接运用米勒定理解题,这将会突破思维瓶颈、大大减少运算量、降低思维难度、缩短解题长度,从而使问题顺利解决。否则这类问题将成为考生的一道难题甚至一筹莫展,即使解出也费时化力。例 1.(2025·广东珠海·九年级统考期末)如图,在足球训练中,小明带球奔向对方球门 PQ,仅从射门角度大小考虑,小明将球传给哪位球员射门较好( )A.甲B.乙C.丙D.丁例 2.(2025·四川宜宾·校考二模)如图,已知点 A、B 的坐标分别是、,点 C 为 x 轴正半轴上一动点,当最大时,点 C 的坐标是( )A.B.C.D.例 3.(2025·江苏南京·九年级统考期中)如图,在矩形 ABCD 中,AB=4,AD=8,M 是 CD 的中点,点P 是 BC 上一个动点,若∠DPM 的度数最大,则 BP= .例 4.(2025·陕西西安·校考模拟预测)足球射门...