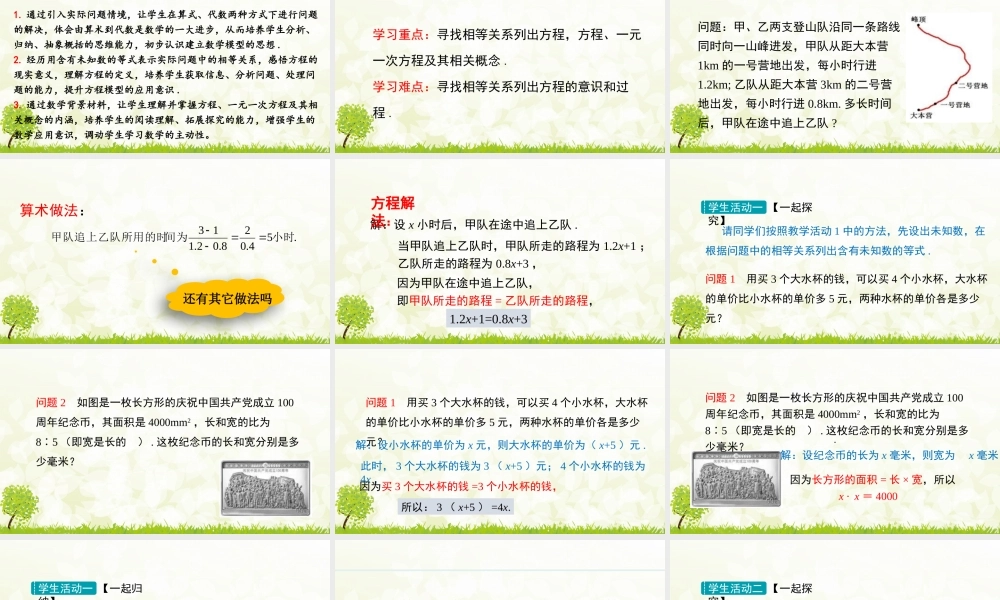
第五章 一元一次方程 5.1 方程 第 1 课时 从算式到方程 1. 通过引入实际问题情境,让学生在算式、代数两种方式下进行问题的解决,体会由算术到代数是数学的一大进步,从而培养学生分析、归纳、抽象概括的思维能力,初步认识建立数学模型的思想 .2. 经历用含有未知数的等式表示实际问题中的相等关系,感悟方程的现实意义,理解方程的定义,培养学生获取信息、分析问题、处理问题的能力,提升方程模型的应用意识 .3. 通过数学背景材料,让学生理解并掌握方程、一元一次方程及其相关概念的内涵,培养学生的阅读理解、拓展探究的能力,增强学生的数学应用意识,调动学生学习数学的主动性。学习重点:寻找相等关系列出方程,方程、一元一次方程及其相关概念 .学习难点:寻找相等关系列出方程的意识和过程 .问题:甲、乙两支登山队沿同一条路线同时向一山峰进发,甲队从距大本营1km 的一号营地出发,每小时行进1.2km; 乙队从距大本营 3km 的二号营地出发,每小时行进 0.8km. 多长时间后,甲队在途中追上乙队 ?.54.028.02.113小时间为甲队追上乙队所用的时算术做法:还有其它做法吗解:设 x 小时后,甲队在途中追上乙队 .方程解法:1.2x+1=0.8x+3当甲队追上乙队时,甲队所走的路程为 1.2x+1 ;乙队所走的路程为 0.8x+3 ,因为甲队在途中追上乙队,即甲队所走的路程 = 乙队所走的路程,请同学们按照教学活动 1 中的方法,先设出未知数,在根据问题中的相等关系列出含有未知数的等式 .问题 1 用买 3 个大水杯的钱,可以买 4 个小水杯,大水杯的单价比小水杯的单价多 5 元,两种水杯的单价各是多少元?学生活动一 【一起探究】问题 2 如图是一枚长方形的庆祝中国共产党成立 100周年纪念币,其面积是 4000mm2 ,长和宽的比为85∶ (即宽是长的 ) . 这枚纪念币的长和宽分别是多少毫米?问题 1 用买 3 个大水杯的钱,可以买 4 个小水杯,大水杯的单价比小水杯的单价多 5 元,两种水杯的单价各是多少元?解:设小水杯的单价为 x 元,则大水杯的单价为( x+5 )元 .此时, 3 个大水杯的钱为 3 ( x+5 )元; 4 个小水杯的钱为4x ,所以: 3 ( x+5 ) =4x.因为买 3 个大水杯的钱 =3 个小水杯的钱,解:设纪念币的长为 x 毫米,则宽为 x 毫米 .因为长方形的面积 = 长 × 宽,所以问题 2 如图是一枚长方形的庆祝中国共产党成立 100周年纪念币,其面积是 ...