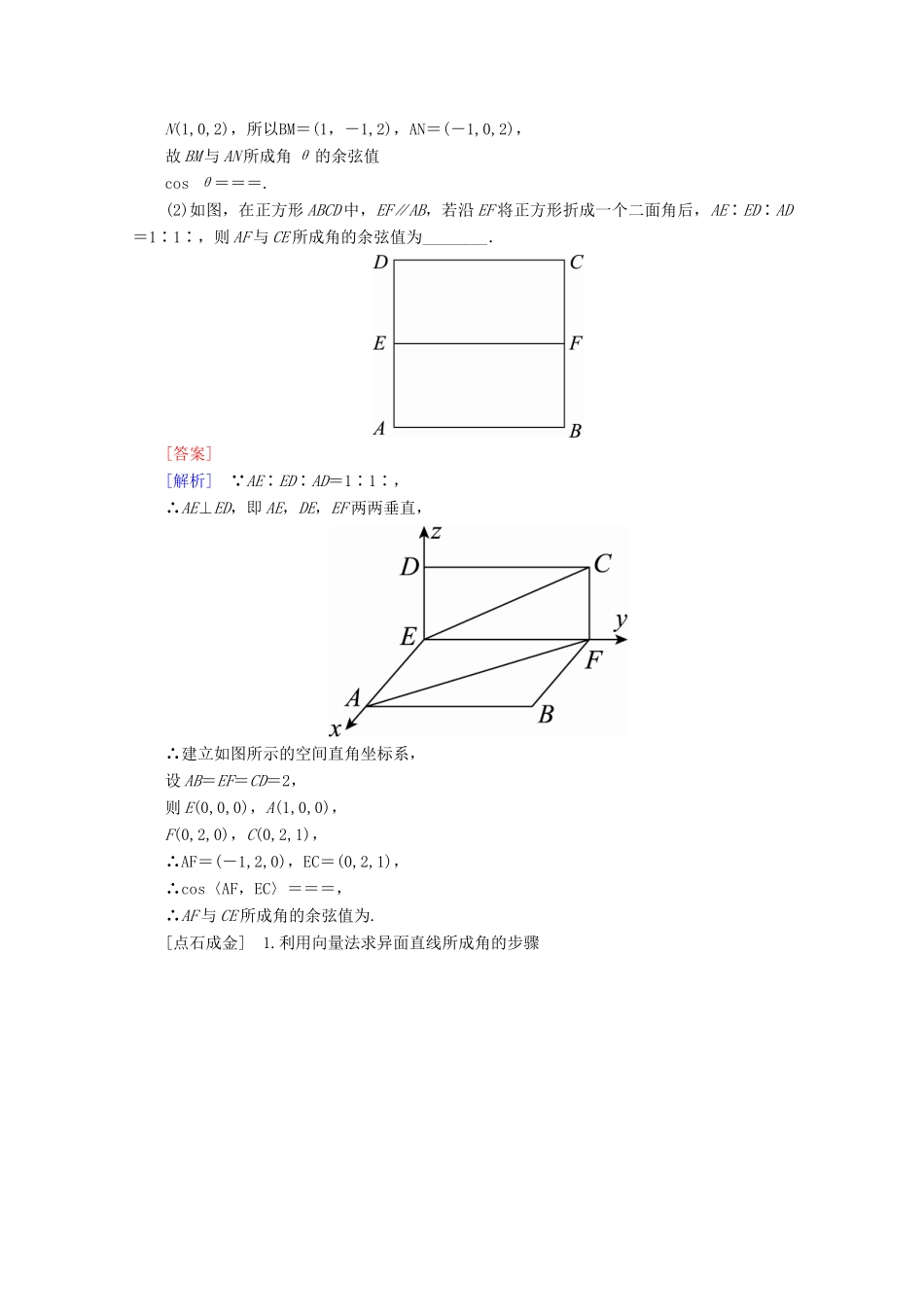
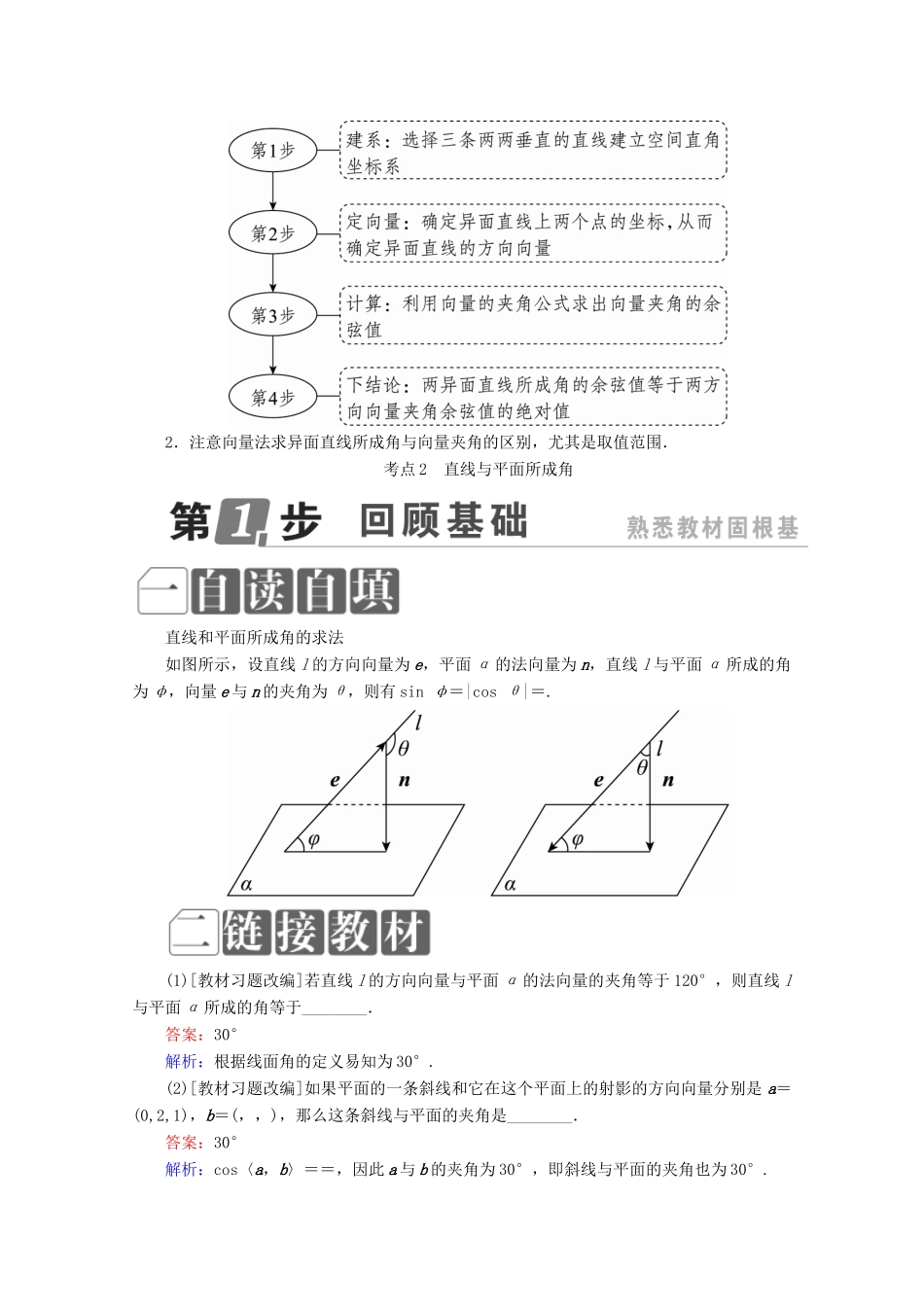
§8.7 利用空间向量求空间角考纲展示► 1.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题.2.了解向量方法在研究立体几何问题中的应用.考点 1 异面直线所成的角两条异面直线所成角的求法设两条异面直线 a,b 的方向向量为 a,b,其夹角为 θ,则 cos φ=|cos θ|=(其中φ 为异面直线 a,b 所成的角).空间角的范围处理错误.已知向量 m,n 分别是直线 l 和平面 α 的方向向量、法向量,若 cos〈m,n〉=-,则 l与 α 所成的角为________.答案:30°解析:设 l 与 α 所成的角为 θ,则 sin θ=|cos〈m,n〉|=,∴θ=30°.[典题 1] (1)直三棱柱 ABC-A1B1C1 中,∠BCA=90°,M,N 分别是 A1B1,A1C1 的中点,BC=CA=CC1,则 BM 与 AN 所成角的余弦值为( )A. B. C. D.[答案] C[解析] 建立如图所示的空间直角坐标系 C-xyz,设 BC=2,则 B(0,2,0),A(2,0,0),M(1,1,2),N(1,0,2),所以BM=(1,-1,2),AN=(-1,0,2),故 BM 与 AN 所成角 θ 的余弦值cos θ===.(2)如图,在正方形 ABCD 中,EF∥AB,若沿 EF 将正方形折成一个二面角后,AE∶ED∶AD=1∶1∶,则 AF 与 CE 所成角的余弦值为________.[答案] [解析] AE∶ED∶AD=1∶1∶,∴AE⊥ED,即 AE,DE,EF 两两垂直,∴建立如图所示的空间直角坐标系,设 AB=EF=CD=2,则 E(0,0,0),A(1,0,0),F(0,2,0),C(0,2,1),∴AF=(-1,2,0),EC=(0,2,1),∴cos〈AF,EC〉===,∴AF 与 CE 所成角的余弦值为.[点石成金] 1.利用向量法求异面直线所成角的步骤2.注意向量法求异面直线所成角与向量夹角的区别,尤其是取值范围.考点 2 直线与平面所成角 直线和平面所成角的求法如图所示,设直线 l 的方向向量为 e,平面 α 的法向量为 n,直线 l 与平面 α 所成的角为 φ,向量 e 与 n 的夹角为 θ,则有 sin φ=|cos θ|=.(1)[教材习题改编]若直线 l 的方向向量与平面 α 的法向量的夹角等于 120°,则直线 l与平面 α 所成的角等于________.答案:30°解析:根据线面角的定义易知为 30°.(2)[教材习题改编]如果平面的一条斜线和它在这个平面上的射影的方向向量分别是 a=(0,2,1),b=(,,),那么这条斜线与平面的夹角是________.答案:30°解析:cos〈a,b〉==,因此 a 与 b 的夹角为 30°,即斜线与平面的夹角也为 30°.(3)[教材习题...