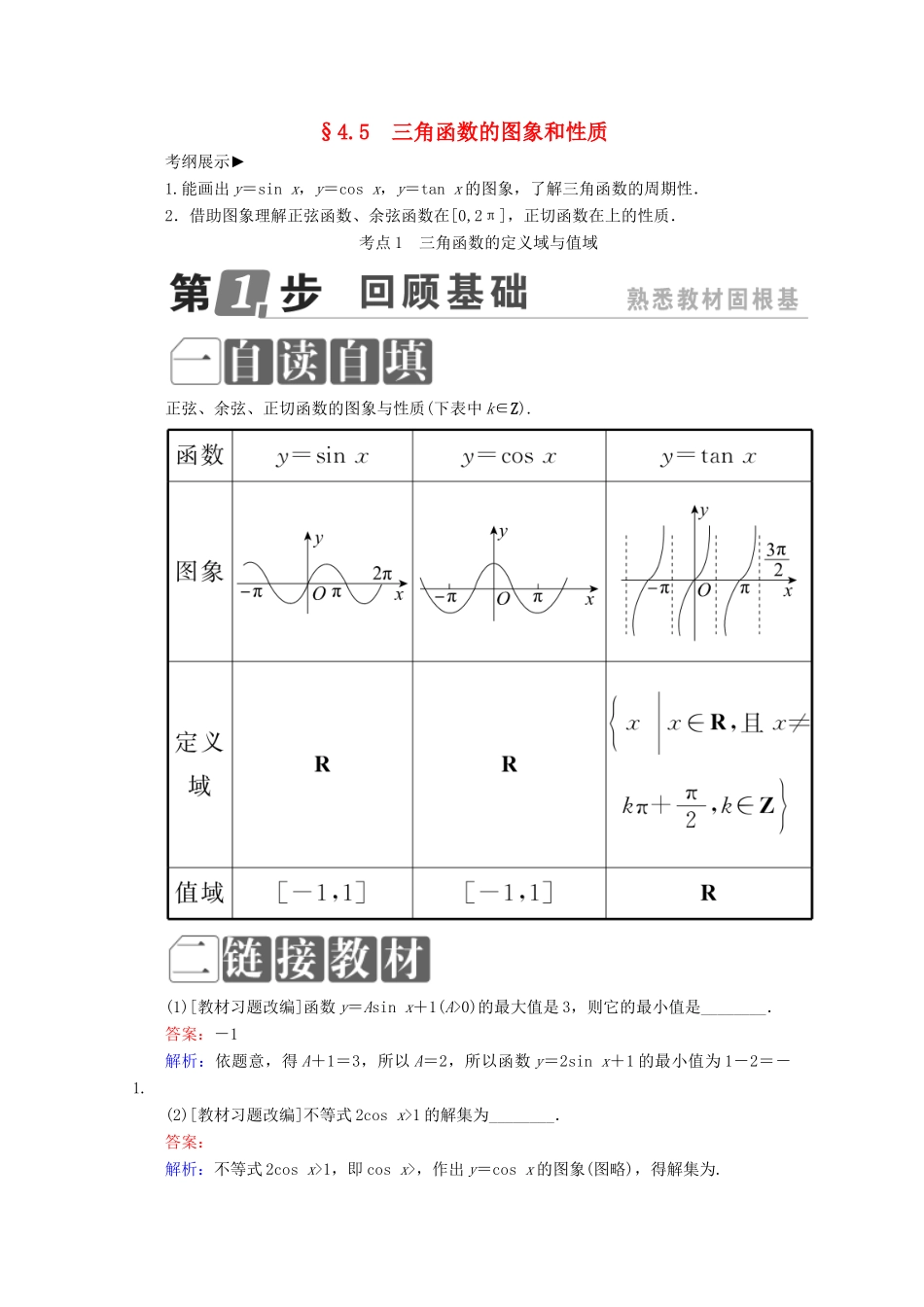
§4.5 三角函数的图象和性质考纲展示► 1.能画出 y=sin x,y=cos x,y=tan x 的图象,了解三角函数的周期性.2.借助图象理解正弦函数、余弦函数在[0,2π],正切函数在上的性质.考点 1 三角函数的定义域与值域正弦、余弦、正切函数的图象与性质(下表中 k∈Z).(1)[教材习题改编]函数 y=Asin x+1(A>0)的最大值是 3,则它的最小值是________.答案:-1解析:依题意,得 A+1=3,所以 A=2,所以函数 y=2sin x+1 的最小值为 1-2=-1.(2)[教材习题改编]不等式 2cos x>1 的解集为________.答案: 解析:不等式 2cos x>1,即 cos x>,作出 y=cos x 的图象(图略),得解集为.求三角函数最值(值域)的两种方法:化为 y=Asin(ωx+φ)的形式来求;换元法.(1)[2013·天津卷改编]函数 f(x)=sin 在区间上的最小值为________.答案:- 解析:由 x∈,得 2x-∈,所以 sin∈,故函数 f(x)=sin 在区间上的最小值为-.(2)已知 x∈,则函数 y=-cos2x+cos x+1 的最小值为________.答案:解析:y=-cos2x+cos x+1=-2+,令 t=cos x,因为 x∈,所以-≤t≤,所以当 t=cos x=-时,ymin=-2+=.[典题 1] (1)函数 y=lg(2sin x-1)+的定义域是________.[答案] ,k∈Z[解析] 要使函数 y=lg(2sin x-1)+有意义,则即解得 2kπ+≤x<2kπ+,k∈Z.即函数的定义域为,k∈Z.(2)函数 y=2sin(0≤x≤9)的最大值与最小值的和为________.[答案] 2-[解析] 0≤x≤9,∴-≤x-≤,∴-≤sin≤1,故-≤2sin≤2.即函数 y=2sin(0≤x≤9)的最大值为 2,最小值为-.所以最大值与最小值的和为 2-.[题点发散 1] 若将本例(2)中的函数换为“y = 3 - sin x - 2cos 2 x ,x∈”,如何解决?解: x∈,∴sin x∈.又 y=3-sin x-2cos2x=3-sin x-2(1-sin2x)=22+,∴当 sin x=时,ymin=;当 sin x=-或 sin x=1 时,ymax=2.故函数的最大值与最小值的和为 2+=.[ 题 点 发 散 2] 若 将 本 例 (2) 中 的 函 数 换 为 “ y = sin x - cos x + sin xcos x,x∈[0,π]”,如何求解?解:令 t=sin x-cos x,又 x∈[0,π],∴t=sin,t∈[-1, ].由 t=sin x-cos x,得 t2=1-2sin xcos x,即 sin xcos x=.∴原函数变为 y=t+,t∈[-1, ].即 y=-t2+t+.∴当 t=1 时,ymax=-...