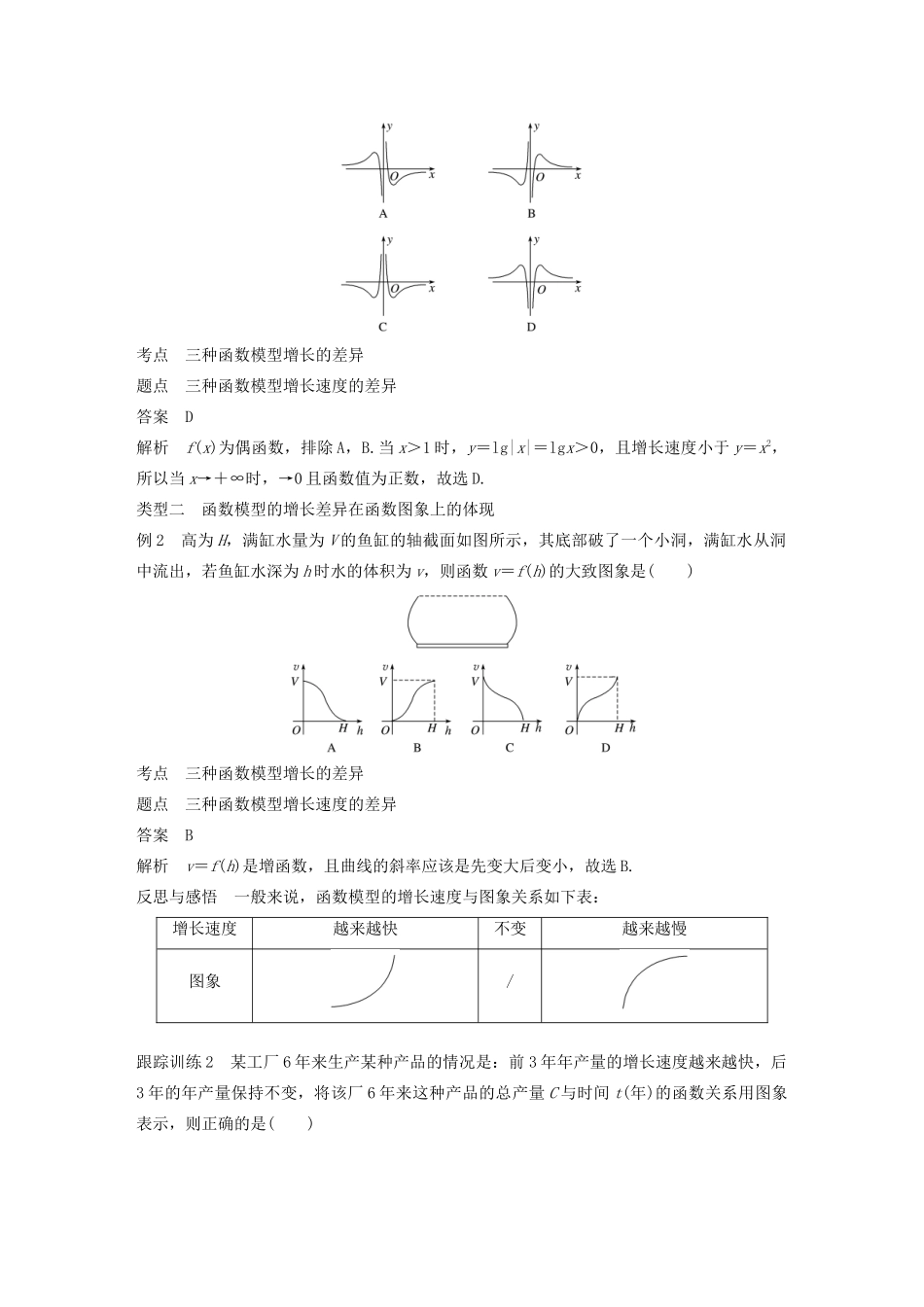
§3.2 函数模型及其应用3.2.1 几类不同增长的函数模型学习目标 1.了解指数函数、对数函数及幂函数等函数模型的增长差异.2.会根据函数的增长差异选择函数模型.知识点一 函数模型一般地,设自变量为 x,函数为 y,并用 x 表示各相关量,然后根据问题的已知条件,运用已掌握的数学知识、物理知识及其他相关知识建立函数关系式,将实际问题转化为数学问题,实现问题的数学化,即所谓建立数学模型.知识点二 三种常见函数模型的增长差异比较三种函数模型的性质,填写下表. 函数性质 y=ax(a>1)y=logax(a>1)y=xn(n>0)在(0,+∞)上的增减性增函数增函数增函数图象的变化随 x 的增大逐渐变“陡”随 x 的增大逐渐趋于稳定随 n 值而不同增长速度ax的增长快于 xn的增长,xn的增长快于 logax 的增长增长后果会存在一个 x0,当 x>x0时,有 a x > x n >log ax1.先有实际问题,后有模型.( √ )2.一个好的函数模型,既能与现有数据高度符合,又能很好地推演和预测.( √ )3.增长速度越来越快的一定是指数函数模型.( × )4.由于指数函数模型增长速度最快,所以对于任意 x∈R 恒有 ax>x2(a>1).( × )类型一 几类函数模型的增长差异例 1 (1)下列函数中,随 x 的增大,增长速度最快的是( )A.y=50xB.y=x50C.y=50xD.y=log50x(x∈N*)考点 三种函数模型增长的差异题点 三种函数模型增长速度的差异答案 C解析 四个函数中,增长速度由慢到快依次是 y=log50x,y=50x,y=x50,y=50x.(2)函数 y=2x-x2的大致图象为( )考点 三种函数模型增长的差异题点 三种函数模型增长速度的差异答案 A解析 在同一平面直角坐标系内作出 y1=2x,y2=x2的图象(图略).易知在区间(0,+∞)上,当 x∈(0,2)时,2x>x2,即此时 y>0;当 x∈(2,4)时,2x<x2,即 y<0;当 x∈(4,+∞)时,2x>x2,即 y>0;当 x=-1 时,y=2-1-1<0.据此可知只有选项 A 中的图象符合条件.反思与感悟 在区间(0,+∞)上,尽管函数 y=ax(a>1),y=logax(a>1)和 y=xn(n>0)都是增函数,但它们的增长速度不同,而且不在同一个“档次”上,随着 x 的增大,y=ax(a>1)的增长速度越来越快,会超过并远远大于 y=xn(n>0)的增长速度,而 y=logax(a>1)的增长速度则会越来越慢.因此,总会存在一个 x0,当 x>x0时,就有 logax<xn<ax.跟踪训练 1 函数 f(x)=的大致图象为( )考点 三种函数模型增长...