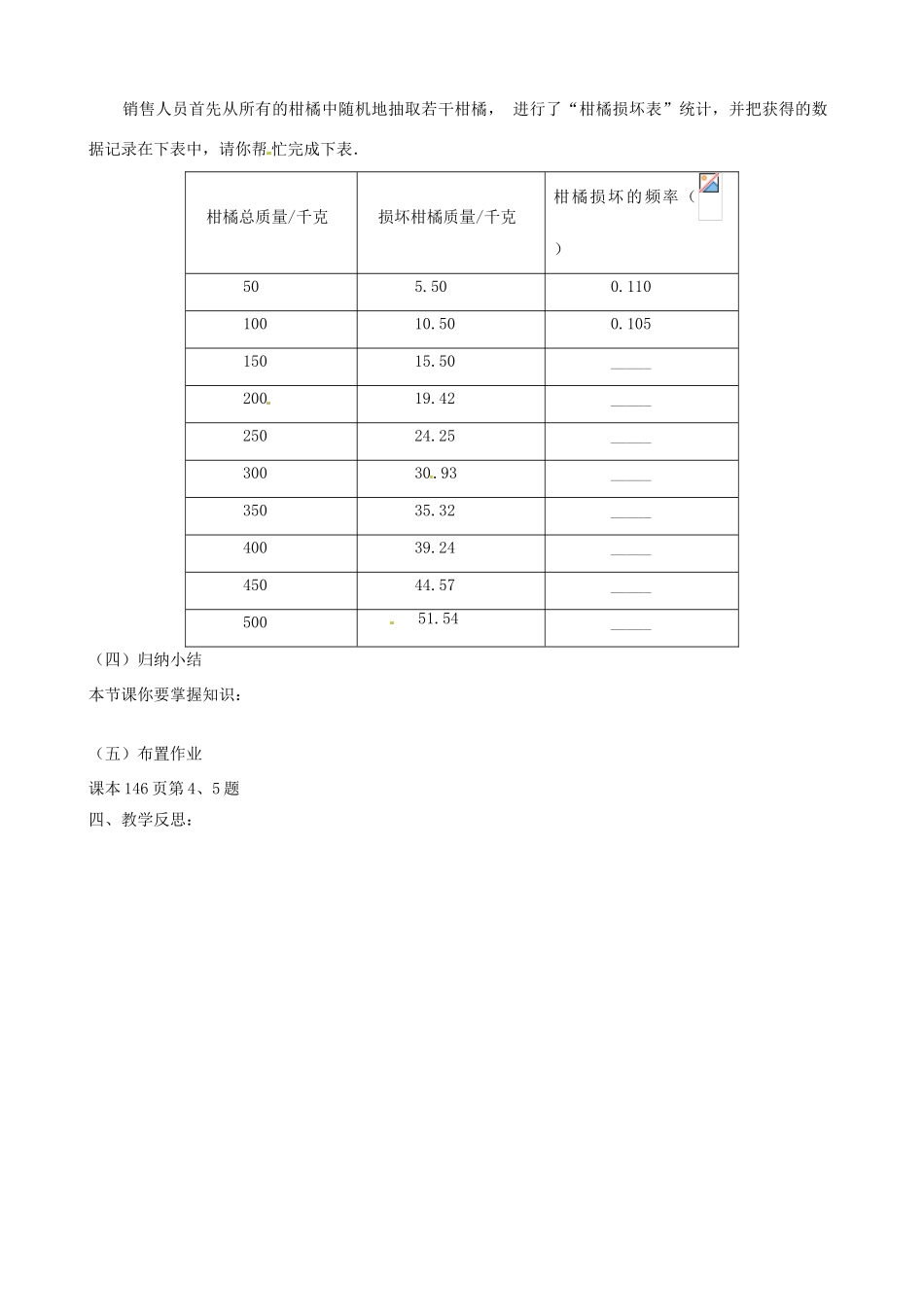
25.2.4用频率估计概率一、教学目标1、通过抛硬币等试验理解当试验次数较大时,随机事件发生的频率所逐渐稳定到的常数可以估计这个事件发生的概率.2、理解概率和频率的内在联系和区别,让学生进一步感受用样本估计总体的统计思想和概率思想.3、通过观察、猜想、试验、归纳、类比等活动,体会数学的应用价值.二、教学重难点重点:理解频率和概率的内在联系和区别,知道当试验次数较大时,频率稳定于概率.难点:在试验中体会随机事件的特点,辩证地理解频率和概率的关系三、教学过程(一)自主学习同学们在前面的学习中,掌握了用P(A)=的理论计算有限等可能随机事件发生的概率.抛掷一枚质地均匀的硬币时,结果是“正面朝上”的概率是多少?解:那么这是否意味着,若投掷20次硬币,是否一定10次“正面朝上”,10次“反面朝上”呢?若抛掷50次、100次、150次呢?我们用试验回答这个问题.概率P(A)=P.(二)课堂点拨1.把全班同学分成10组,每组同学掷一枚硬币50次,整理同学们获得的试验数据,并记录在表中.第1组的数据填在第1列,第1,2组的数据之和填在第2列,···,10个组的数据之和填在第10列.如果在抛掷n次硬币时,出现m次“正面朝上”,则随机事件“正面朝上”出现的频率为抛掷次数n50100150200250300350400450500正面朝上的频数m正面朝上的频率根据上表中的数据,在所给的坐标系中标注对应的点.请同学们根据试验数据想一想:“正面朝上”的频率有什么规律?归纳:(1)每次试验中随机事件发生的频率具有不确定性.(2)在试验次数较少时,“正面朝上”的频率可能起伏较大,随着试验次数的增加,频率呈现出一定的稳定性,在0.5左右摆动的幅度会越来越小,“正面朝上”的频率稳定于0.5.历史上,有些人曾做过成千上万抛掷硬币的试验,结果如下表:试验者投掷次数(n)正面朝上的频数(m)正面朝上的频率()棣莫弗204810610.518布丰404020480.5069费勒1000049790.4979皮尔逊1200060190.5016皮尔逊24000120120.5005从表中进一步证实了我们所作的推断,随着抛掷次数的增加,“正面朝上”的频率稳定于当“正面朝上”的频率稳定于0.5时,“反面朝上”的频率呈现什么规律?答:归纳:一般地,在大量重复试验中,如果事件A发生的频率稳定于某一个常数P那么事件A发生的概率P(A)=P.(三)当堂训练1.在做布斗的投针实验时,若改变平行线间的距离与针的长度的比值,则()A.针与平行线相交的概率不变B.针与平行线相交的概率会改变C.针与平行线相交的概率可能会改变;D.以上说法都不对2.当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,求(估计)概率是用().A.通过统计频率估计概率B.用列举法求概率C.用列表法求概率D.用树形图法求概率3.布斗投针实验的概率是.4.事件发生的概率随着的增加,逐渐在某个数值附近,我们可以用平稳时来估计这一事情的概率.5.一个学习小组有6名男生3名女生,老师要从小组的学生中先后随机地抽取3人参加几项测试,并且每名学生都可被重复抽取,你能设计一种试验来估计“被抽取的3人中有2名男生1名女生”的概率吗?6.某水果公司以2元/千克的成本新进了10000千克的柑橘,如果公司希望这种柑橘能够获得利润5000元,那么在出售柑橘(已经去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏表”统计,并把获得的数据记录在下表中,请你帮忙完成下表.柑橘总质量/千克损坏柑橘质量/千克柑橘损坏的频率()505.500.11010010.500.10515015.50_____20019.42_____25024.25_____30030.93_____35035.32_____40039.24_____45044.57_____50051.54_____(四)归纳小结本节课你要掌握知识:(五)布置作业课本146页第4、5题四、教学反思: