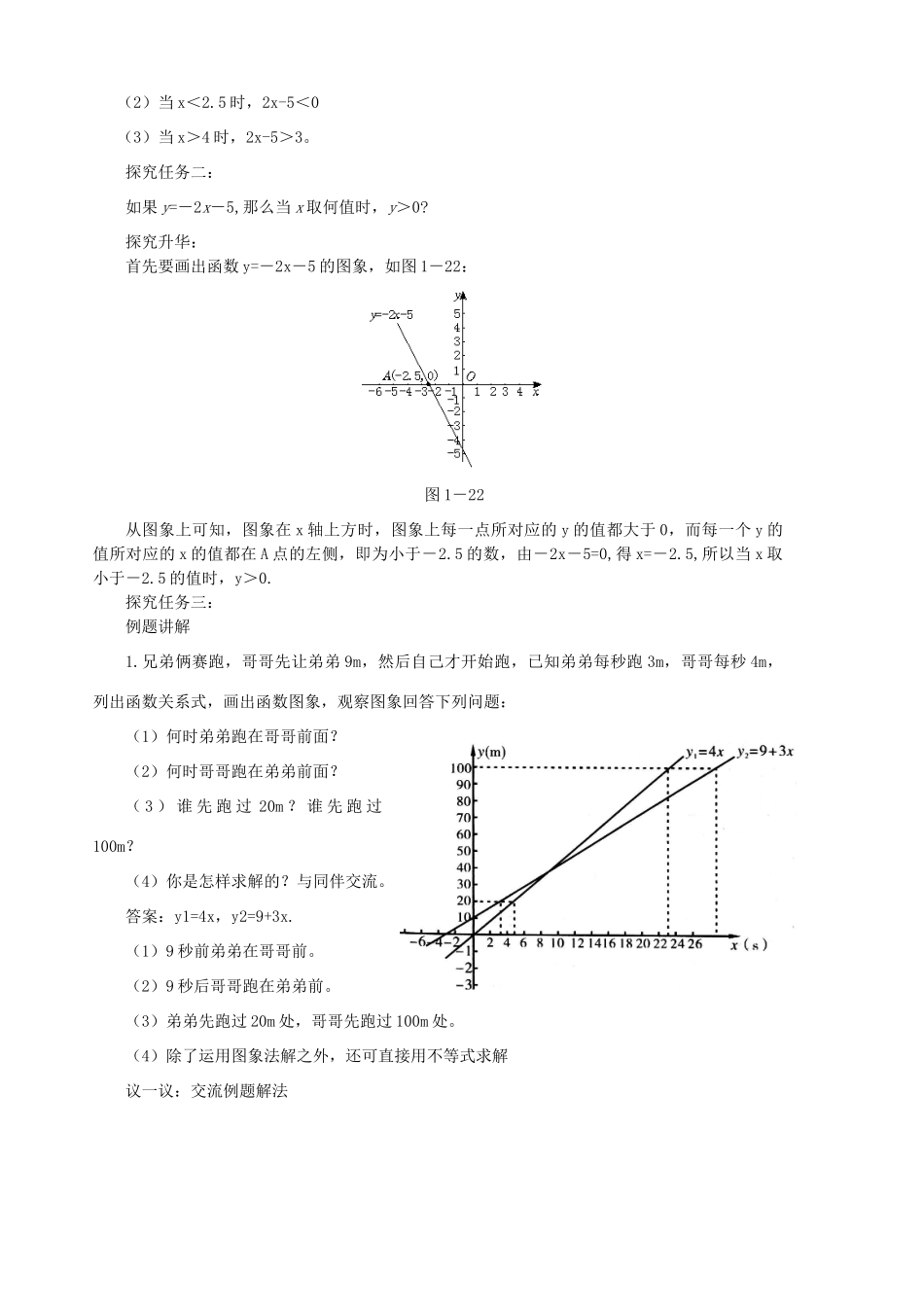
八年级数学导学案课题:1.51一元一次不等式与一次函数学习目标:(一)教学知识点1.一元一次不等式与一次函数的关系.2.会根据题意列出函数关系式,画出函数图象,并利用不等关系进行比较.(二)能力训练要求1.通过一元一次不等式与一次函数的图象之间的结合,培养学生的数形结合意识.2.训练大家能利用数学知识去解决实际问题的能力.(三)情感与价值观要求体验数、图形是有效地描述现实世界的重要手段,认识到数学是解决问题和进行交流的重要工具,了解数学对促进社会进步和发展人类理性精神的作用.●教学重点了解一元一次不等式与一次函数之间的关系.●教学难点自己根据题意列函数关系式,并能把函数关系式与一元一次不等式联系起来作答.一、课前准备(预习教材P20-P21,找出疑惑之处)一元一次不等式的解法、一次函数的图像与性质二、新课导学创设问题情境,引入新课上节课我们学习了一元一次不等式的解法,那么,是不是不等式的知识是孤立的呢?本节课我们来研究不等式的有关应用.互动探究探究任务一:1.作出函数y=2x-5的图象,观察图象回答下列问题:(1)x取哪些值时,2x-5>0?(2)x取哪些值时,2x-5<0?(3)x取哪些值时,2x-5>3?答案:(1)当x>2.5时,2x-5>0。(2)当x<2.5时,2x-5<0(3)当x>4时,2x-5>3。探究任务二:如果y=-2x-5,那么当x取何值时,y>0?探究升华:首先要画出函数y=-2x-5的图象,如图1-22:图1-22从图象上可知,图象在x轴上方时,图象上每一点所对应的y的值都大于0,而每一个y的值所对应的x的值都在A点的左侧,即为小于-2.5的数,由-2x-5=0,得x=-2.5,所以当x取小于-2.5的值时,y>0.探究任务三:例题讲解1.兄弟俩赛跑,哥哥先让弟弟9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒4m,列出函数关系式,画出函数图象,观察图象回答下列问题:(1)何时弟弟跑在哥哥前面?(2)何时哥哥跑在弟弟前面?(3)谁先跑过20m?谁先跑过100m?(4)你是怎样求解的?与同伴交流。答案:y1=4x,y2=9+3x.(1)9秒前弟弟在哥哥前。(2)9秒后哥哥跑在弟弟前。(3)弟弟先跑过20m处,哥哥先跑过100m处。(4)除了运用图象法解之外,还可直接用不等式求解议一议:交流例题解法随堂练习:1三、总结提升学习小结:本节课讨论了一元一次不等式与一次函数的关系,并且能根据一次函数的图象求解不等式.知识拓展:作出函数y1=2x-4与y2=-2x+8的图象,并观察图象回答下列问题:(1)x取何值时,2x-4>0?(2)x取何值时,-2x+8>0?(3)x取何值时,2x-4>0与-2x+8>0同时成立?(4)你能求出函数y1=2x-4,y2=-2x+8的图象与x轴所围成的三角形的面积吗?并写出过程.解:图象如下:图1-25分析:要使2x-4>0成立,就是y1=2x-4的图象在x轴上方的所有点的横坐标的集合,同理使-2x+8>0成立的x,即为函数y2=-2x+8的图象在x轴上方的所有点的横坐标的集合,要使它们同时成立,即求这两个集合中公共的x,根据函数图象与x轴交点的坐标可求出三角形的底边长,由两函数的交点坐标可求出底边上的高,从而求出三角形的面积.[解](1)当x>2时,2x-4>0;(2)当x<4时,-2x+8>0;(3)当2<x<4时,2x-4>0与-2x+8>0同时成立.(4)由2x-4=0,得x=2;由-2x+8=0,得x=4所以AB=4-2=2由得交点C(3,2)所以三角形ABC中AB边上的高为2.所以S=×2×2=2.当堂检测:1.某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现:如果月初出售,可获利15%,并可用本和利再投资其他商品,到月末又可获利10%;如果月末出售可获利30%,但要付出仓储费用700元.请问根据商场的资金状况,如何购销获利较多?解:设商场计划投入资金为x元,在月初出售,到月末共获利y1元;在月末一次性出售获利y2元,根据题意,得y1=15%x+(x+15%x)·10%=0.265x,y2=30%x-700=0.3x-700.(1)当y1>y2,即0.265x>0.3x-700时,x<20000;(2)当y1=y2,即0.265x=0.3x-700时,x=20000;(3)当y1<y2,即0.265x<0.3x-700时,x>20000.所以,当投入资金不超过20000元时,第一种销售方式获利较多;当投入资金超过20000元时,第二种销售方式获利较多.课后作业:CT1.6学习评价:自我评价你完成本节导学案的情况为()A、很好B、较好C、一般D、较差