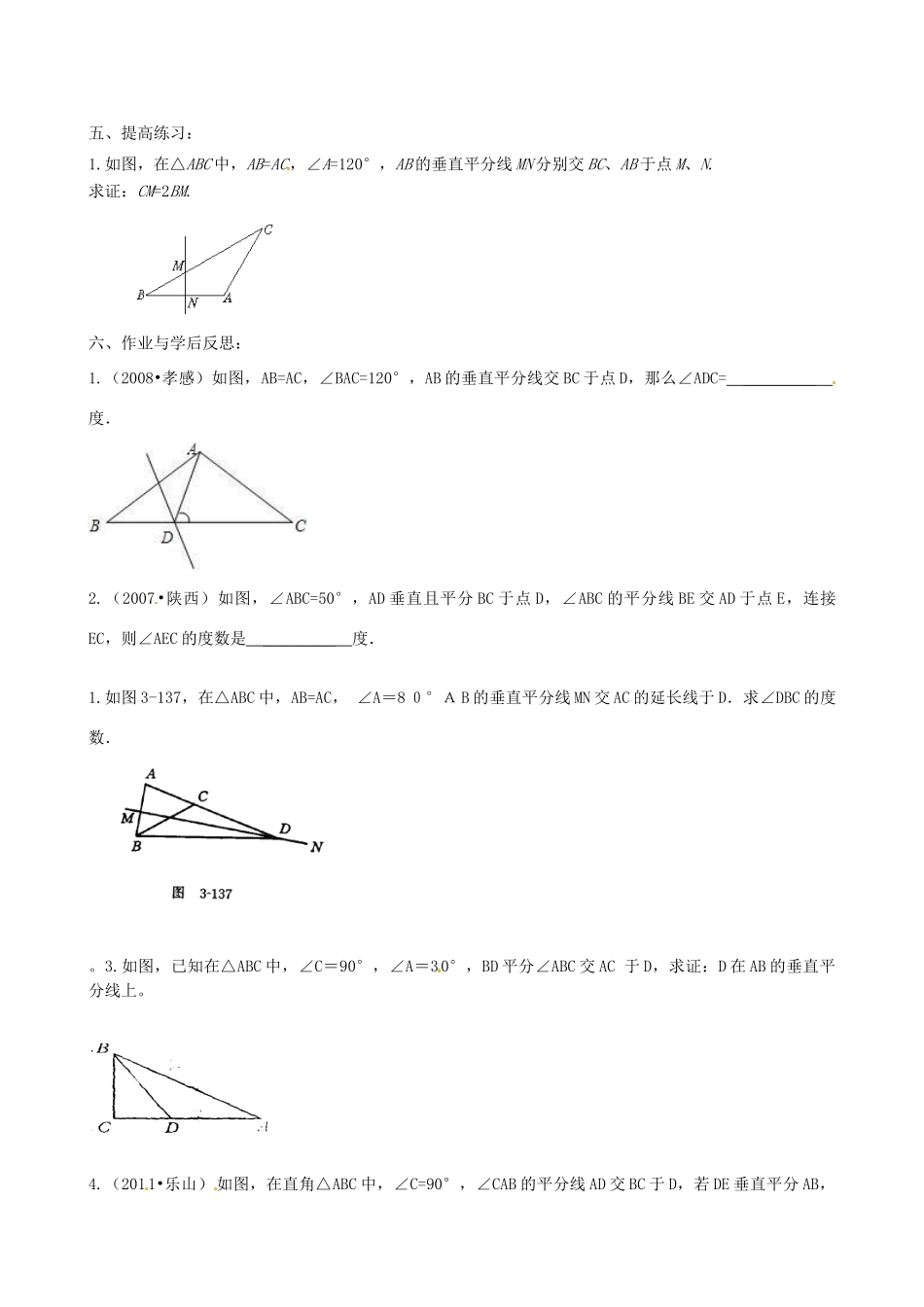
八年级数学上册导学案(八)轴对称(二)——垂直平分线的性质【教学目标】:1.要求学生掌握线段垂直平分线的性质定理及判定定理,能够利用这两个定理解决一些问题。2.能够证明线段垂直平分线的性质定理及判定定理。【教学重难点】:线段垂直平分线的性质定理及其逆定理的内涵和证明。【自学指导】:一、学生看P32---P35并思考一下问题:1)线段垂直平分线的性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等,按照要求写出已知求证,明确题意,积极思考命题的证法。2)可以证明线段相等方法目前我们掌握了哪几种?3)线段垂直平分线的判定定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上,写出已知和求证并证明逆定理,解释几何意义。4)引导学生回忆第二节课学过的关于互逆命题和互逆定理的知识,让学生说出自己收集的数学上的互逆命题和互逆定理。5)如何用尺规作图作线段的垂直平分线?写出已知、求作、作法,体会作法中每一步的依据.二、自学检测:1、(2010•台湾)如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下:(甲)作∠ACP、∠BCP之角平分线,分别交AB于D、E,则D、E即为所求;(乙)作AC、BC之中垂线,分别交AB于D、E,则D、E即为所求.对于甲、乙两人的作法,下列判断何者正确()A、两人都正确B、两人都错误C、甲正确,乙错误D、甲错误,乙正确2、(2010•三明)如图,在Rt△ABC中,∠C=90°,∠B=30°.AB的垂直平分线DE交AB于点D,交BC于点E,则下列结论不正确的是()A、AE=BEB、AC=BEC、CE=DED、∠CAE=∠B3.如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建在什么位置?4.已知,D是直角斜边AC的中点,于D交BC于E,,求:的度数。三、师生共同探讨,总结:a)线段垂直平分线上的点和这条线段两个端点的距离相等,可见,定理是证明两线段相等的依据。b)逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。可见,逆定理是证明点在直线上的依据.c)线段的垂直平分线可以看作是和这条线段的两个端点的距离相等的所有的点的集合。四、例题讲解:P34例题五、提高练习:1.如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN分别交BC、AB于点M、N.求证:CM=2BM.六、作业与学后反思:1.(2008•孝感)如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠ADC=_________度.2.(2007•陕西)如图,∠ABC=50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是_________度.1.如图3-137,在△ABC中,AB=AC,∠A=80°AB的垂直平分线MN交AC的延长线于D.求∠DBC的度数.。3.如图,已知在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC交AC于D,求证:D在AB的垂直平分线上。4.(2011•乐山)如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.5、(2010•娄底)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:(1)FC=AD;(2)AB=BC+AD.在这一节中,所介绍的定理实际是在七年级曾经探索过的命题,如线段垂直平分线的性质定理,作为探索活动的自然延续和必要发展,我们作为老师要善于引导学生从问题出发,根据观察、实验的结果先得出猜想,然后再进行证明,要求学生掌握证明的基本要求和方法,注意数学压想方法的强化和渗透.