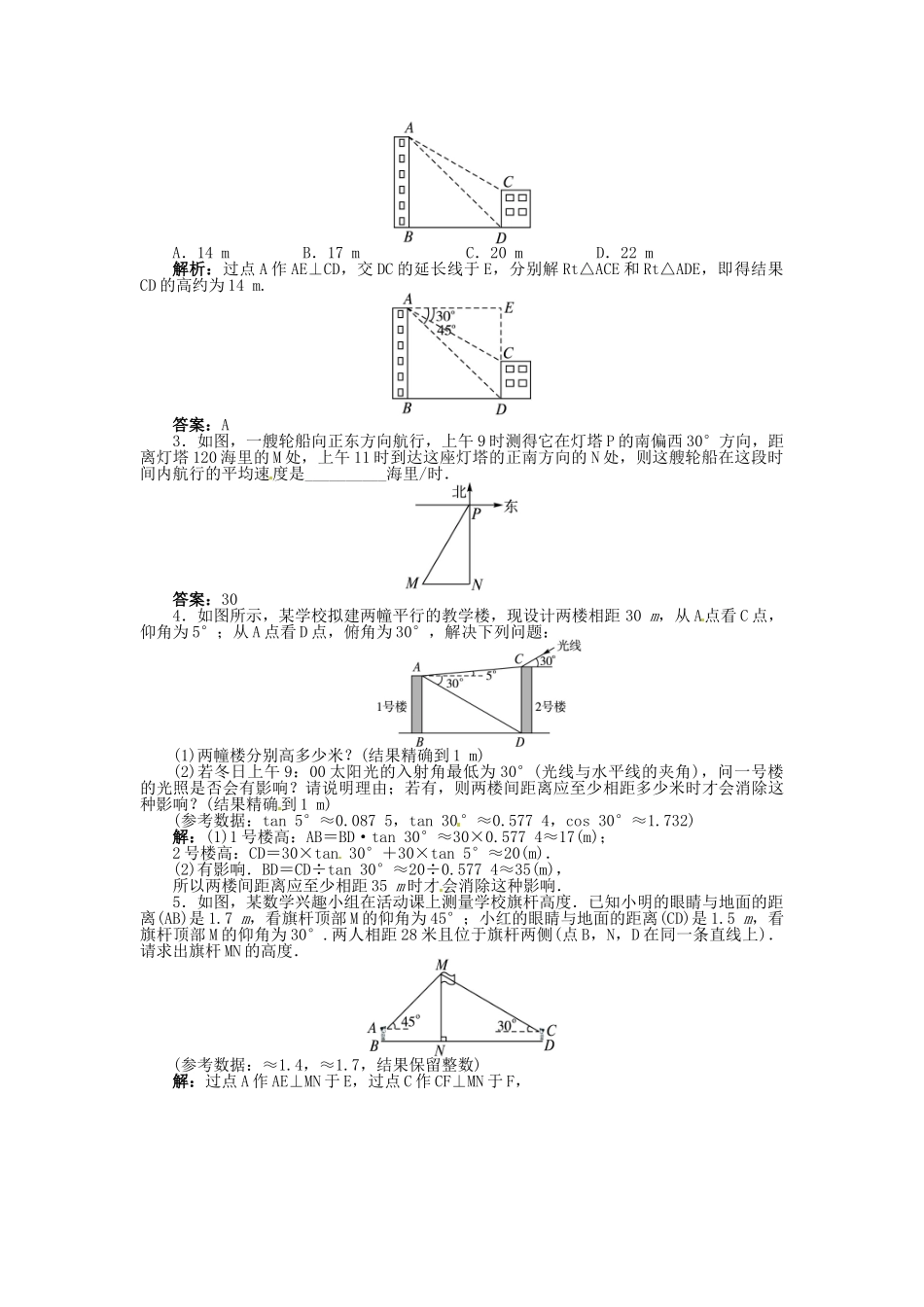
第3课时解直角三角形的应用(2)1.利用解直角三角形的知识解决实际问题的一般过程是:(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;(3)得到数学问题的答案;(4)得到实际问题的答案.2.如图,已知一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距().A.25海里B.30海里C.35海里D.40海里答案:D1.作三角形的高构造两个直角三角形解决实际问题【例1】热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为66m,则这栋高楼有多高?(结果精确到0.1m,参考数据:≈1.73)分析:过点A作AD⊥BC,构造出两个Rt△ADB和Rt△ADC.解:如图,过点A作AD⊥BC,垂足为D.根据题意,可得∠BAD=30°,∠CAD=60°,AD=66m.在Rt△ADB中,由tan∠BAD=,得BD=AD·tan∠BAD=66×tan30°=66×=22(m).在Rt△ADC中,由tan∠CAD=,得CD=AD·tan∠CAD=66×tan60°=66×=66(m).∴BC=BD+CD=22+66=88≈152.2(m).答:这栋楼高约为152.2m.对于复杂的三角形,通常作辅助线,将已知条件与所解决的问题联系在两个直角三角形中.针对性训练见当堂检测·基础达标栏目第5题2.作垂线构造两个重叠的直角三角形解决实际问题【例2】某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距3m,探测线与地面的夹角分别是30°和60°(如图),试确定生命所在点C的深度.(结果精确到0.1m,参考数据:≈1.41,≈1.73)分析:生命所在点C的深度就是点C距地面的距离,过点C作CD⊥AB交AB于D,构造出Rt△BDC和Rt△ADC.解:如图,过点C作CD⊥AB交AB于D,∵探测线与地面的夹角为30°或60°,∴∠CAD=30°,∠CBD=60°.在Rt△BDC中,tan60°=,∴BD==.在Rt△ADC中,tan30°=,∴AD==.∵AB=AD-DB=3,∴-=3.∴CD=≈≈2.6(m).∴生命所在点C的深度约为2.6m.归纳本题可以得出这类问题的通用方法,在下图所示的一个基本图形中,x=.针对性训练见当堂检测·基础达标栏目第2题1.如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60度500m处,那么水塔所在的位置到公路的距离AB是().A.250mB.250mC.mD.250m答案:A2.如图,两建筑物水平距离为32m,从点A测得对点C的俯角为30°,对点D的俯角为45°,则建筑物CD的高约为().A.14mB.17mC.20mD.22m解析:过点A作AE⊥CD,交DC的延长线于E,分别解Rt△ACE和Rt△ADE,即得结果CD的高约为14m.答案:A3.如图,一艘轮船向正东方向航行,上午9时测得它在灯塔P的南偏西30°方向,距离灯塔120海里的M处,上午11时到达这座灯塔的正南方向的N处,则这艘轮船在这段时间内航行的平均速度是__________海里/时.答案:304.如图所示,某学校拟建两幢平行的教学楼,现设计两楼相距30m,从A点看C点,仰角为5°;从A点看D点,俯角为30°,解决下列问题:(1)两幢楼分别高多少米?(结果精确到1m)(2)若冬日上午9:00太阳光的入射角最低为30°(光线与水平线的夹角),问一号楼的光照是否会有影响?请说明理由;若有,则两楼间距离应至少相距多少米时才会消除这种影响?(结果精确到1m)(参考数据:tan5°≈0.0875,tan30°≈0.5774,cos30°≈1.732)解:(1)1号楼高:AB=BD·tan30°≈30×0.5774≈17(m);2号楼高:CD=30×tan30°+30×tan5°≈20(m).(2)有影响.BD=CD÷tan30°≈20÷0.5774≈35(m),所以两楼间距离应至少相距35m时才会消除这种影响.5.如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30°.两人相距28米且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.(参考数据:≈1.4,≈1.7,结果保留整数)解:过点A作AE⊥MN于E,过点C作CF⊥MN于F,则EF=AB-CD=1.7-1.5=0.2(m).在Rt△AEM中,∠AEM=90°,∠MAE=45°,∴AE=ME.设AE=ME=x,∴MF=x+0.2,FC=28-x.在Rt△MFC中,∠MFC=90°,∠MCF=30°,∴MF=CF·tan∠MCF.∴x+0.2=(28-x).∴x≈10.0.∴MN≈12(m).答:旗杆高约为12m.