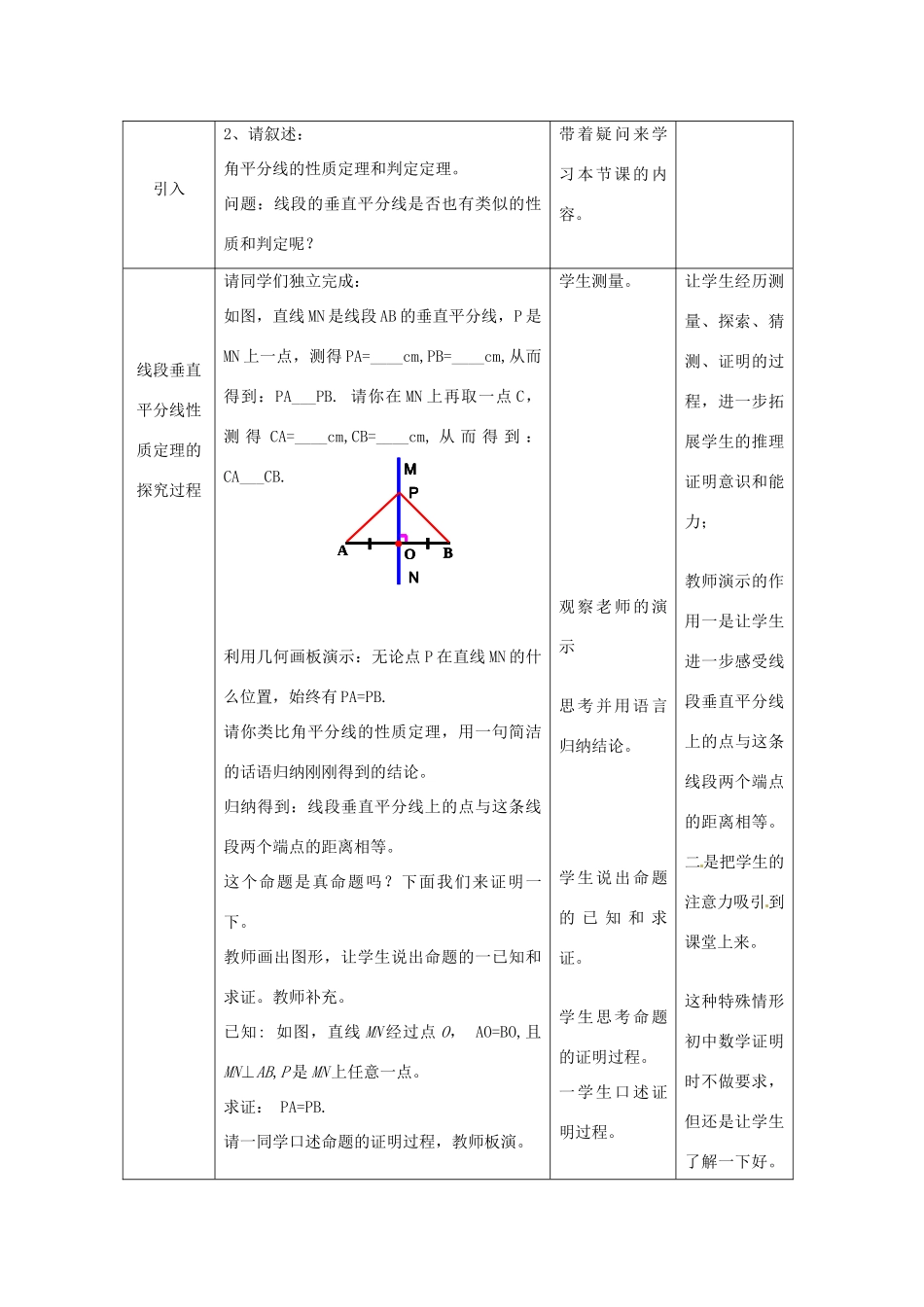
12.1轴对称(第2课时)——线段的垂直平分线【指导思想】新课程理念下的数学教学将由“关注学生学习结果”,转向“关注学生活动”、“重塑知识的形成过程”,课程设计、实施将由“给出知识”转向“引导活动”。倡导学生主动探索,自主学习,合作讨论,体现数学再发现的过程,数学教学不再是教师向学生传授知识的过程,而是给学生创造环境,鼓励学生“观察”、“操作”、“发现”,在这个过程中通过合作交流,让学生发展自主学习的能力,发展学生的个性品质,从而激发学生的学习兴趣,提高学生学习数学的能力。那么在新课程理念下我们应该怎样做呢?做些什么呢?我个人认为,可以从以下几个方面来做。首先、学习兴趣的培养其次、注重数学思想方法教学第三、思维能力的培养第四、口语表达能力的培养第五、应用数学能力的培养第六、非智力因素的培养【教材分析】(一)教材地位本节课是新人教版《数学》八年级上册第十二章第一节轴对称的第二课时(本人对教材做了一定的调整,把线段垂直平分线的的定义和轴对称的性质并入第一课时),这节课可进一步加深学生对轴对称图形的认识,让学生进一步感受全等三角形判定和性质的应用。这节课也是后面将要学习的等腰三角形的基础,一是学习几何图形的方法(定义、性质、判定),二、在证明判定定理时添加的辅助线也是等腰三角形性质和判定证明时常用的辅助线,三、线段垂直平分线的几何图形本身就含有等腰三角形,所以,经常结合等腰三角形来考察线段的垂直平分线。(二)课标解读经历探索、证明线段的垂直平分线的性质定理及其逆定理,并能应用定理解决一些简单的数学问题。定理反映了线段垂直平分线的性质,是证明两条线段相等的依据;逆定理反映了线段垂直平分线的判定,是证明某点在某条直线上及一条直线是已知线段的垂直平分线的依据。(三)教学目标:1、知识目标:(1)掌握线段的垂直平分线的性质定理、判定定理的内涵和证明;(2)能运用它们证明两条线段相等或一条直线是某条线段的垂直平分线。2、能力目标:(1)经历测量、探索、猜测、证明的过程,进一步拓展学生的推理证明意识和能力;(2)通过例题的学习,提高学生的逻辑思维能力及分析问题解决问题的能力;(3)提高综合运用知识的能力。3、情感目标:(1)通过自主学习的发展体验获取数学知识的感受;(2)通过知识的纵横迁移感受数学的辩证特征。(四)教学重点、难点教学重点:线段垂直平分线定理及判定定理的证明、应用。教学难点:线段垂直平分线的性质定理及其逆定理的内涵和证明。教学用具:三角板,电脑课件等(五)教学方法:以学生为主体的归纳探究法【学情分析】心理方面,八年级的学生可塑性大,有着强烈的好奇心和探究欲,喜欢主动尝试。但与七年级知识相比,八年级的知识内容要深得多﹑难得多。同学们在学习方面面临着更大的挑战,有的学生因此产生了畏难情绪,感觉学习吃力,上课听不懂﹑跟不上,由此失去了学习的兴趣。基于此,这节课注重培养学生的学习兴趣,让学生主动参与学习,表达自己的观点。知识方面,学生已经掌握全等三角形的判定和性质,能熟练应用全等三角形的判定和性质证明两条线段相等和两角相等,具有一定的数学思维和数学语言表达能力,所以,探索、猜测、归纳、证明两个定理,在老师的引导下,能顺利完成。【教学过程】活动过程教师活动学生活动设计意图复习1、什么叫线段的垂直平分线?回答问题温故而知新引入2、请叙述:角平分线的性质定理和判定定理。问题:线段的垂直平分线是否也有类似的性质和判定呢?带着疑问来学习本节课的内容。线段垂直平分线性质定理的探究过程请同学们独立完成:如图,直线MN是线段AB的垂直平分线,P是MN上一点,测得PA=____cm,PB=____cm,从而得到:PA___PB.请你在MN上再取一点C,测得CA=____cm,CB=____cm,从而得到:CA___CB.利用几何画板演示:无论点P在直线MN的什么位置,始终有PA=PB.请你类比角平分线的性质定理,用一句简洁的话语归纳刚刚得到的结论。归纳得到:线段垂直平分线上的点与这条线段两个端点的距离相等。这个命题是真命题吗?下面我们来证明一下。教师画出图形,让学生说出命题的一已知和求证。...