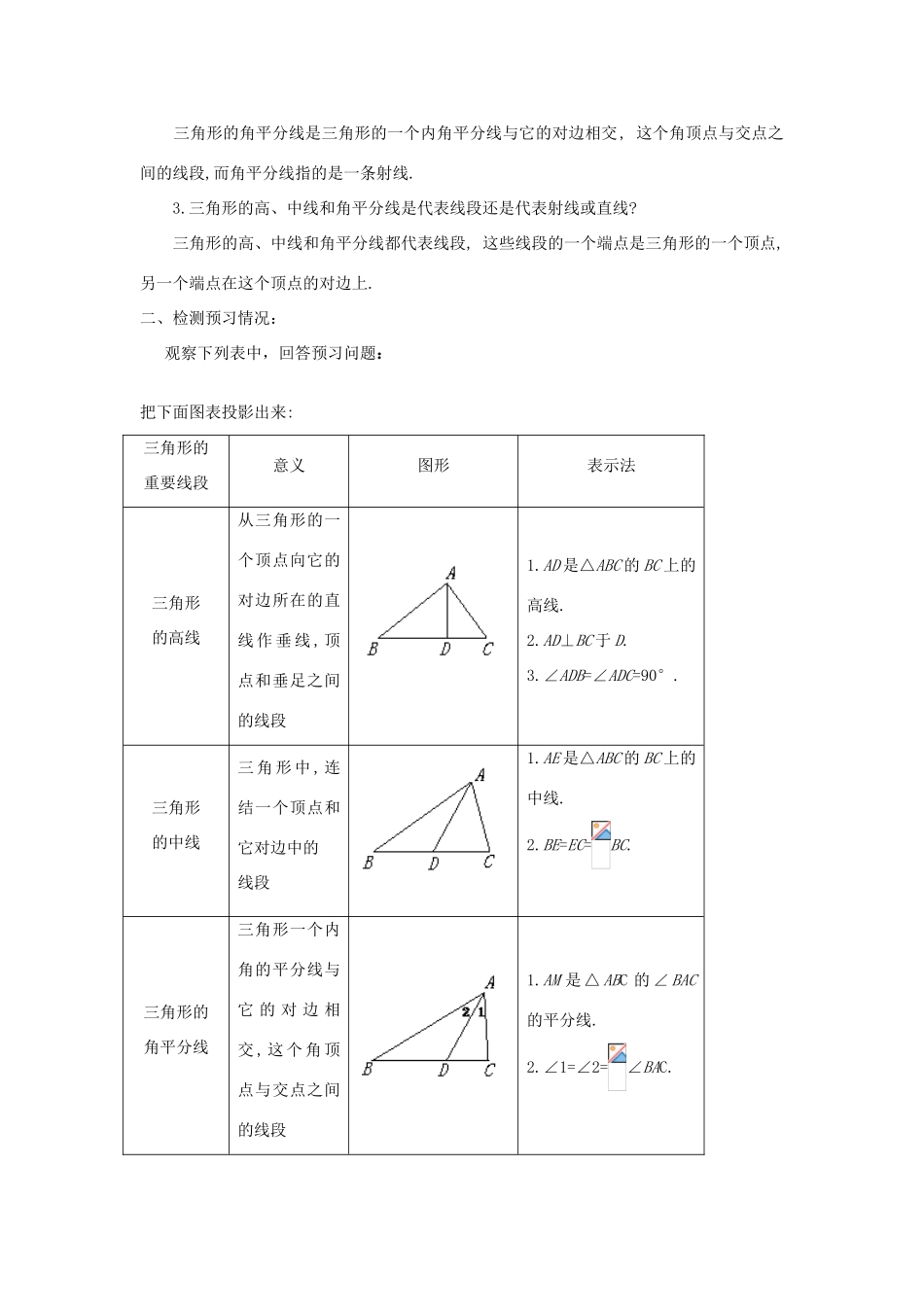
课案(教师用)课题:三角形的高、中线与角平分线(课型新授)【理论支持】《数学课程标准》指出:对学生数学学习的评价,既要关注学生学习的结果,更要关注学生在学习过程中的变化和发展;既要关注学生数学学习的水平,更要关注他们在数学实践活动中所表现出来的情感和态度。从以皮亚杰为代表的建构主义的观点看,学生是主动建构他们自己的知识和对事物作出理解,不是被动地去接受知识。在数学教学中,应该鼓励学生根据自己已有的经验(知识)去经历学习过程,用他们自己理解的方式去探索和重建数学知识,这就是实现“再创造”(即生成)。作为数学老师,必须把一些概念、规律纳入“待解决的问题”情境中,给学生留下足够的思维空间,引导他们经过协商自己去“再创造”,并根据学生的反馈信息,有的放矢地找准新的切入口,抓住重点,有针对性地再现关键问题,把问题再一次设在学生的最近发展区,进行关键突破,抓到“痒”点,从而提高单位时间内课堂效率,事半功倍。本节课根据学生在小学对三角形及高的初步认识,通过画图引申出更深的知识内容,让学生产生对三角形有进一步研究的意识,从而推动下面的教学。在研究三角形的高、中线、角平分线的规律时,我们体现动态教学。我们认为学生学习知识是一个逐步形成的动态生成过程,我们本着“以学定教”的原则建立了动态生成课堂的流程。课前预设关注学生是否“能动”(了解学生的现有的认知水平,生活经验,准确把握学生的最近发展区使“有效地动”成为可能);情境问题、任务构成“驱动”(挑战性的问题、有趣的任务最能驱动学生的思维与行动);由此产生的课堂教学“生动”的智能建构过程(这里强调的是师生、生生间的协商互动促进生成,加强的是教师无痕地点拨,适时地调控,让学生“会动”,体现的是自然、生态的生命过程。);值得一提的是课后总结从形式上的老师总结改为学生总结,从内容上也有了一定的突破,教师指导学生掌握知识的同时,关注学生的诸方面的学习品质的培养,如观察、操作、分析、判断……,其中一项为人们所忽视,那就是指导学生把自己的学习也作为认知对象,理解、反思自己学习的全过程,掌握学习的方法和解题策略,促进“会动”,为真正的学会学习日积月累。教学目标1.经历析纸,画图等实践过程认识三角形的高、中线与角平分线.2.会用工具准确画出三角形的高、中线与角平分线,通过画图了解三角形的三条高(及所在直线)交于一点,三角形的三条中线,三条角平分线等都交于点.3.通过学生作图、观察、比较、描述图形等数学活动,让学生感受数学的严谨性,图形中蕴含的规律性,提高学生学习数学的热情及大担探究新知识的创新能力.重点、难点1.重点:(1)了解三角形的高、中线与角平分线的概念,会用工具准确画出三角形的高、中线与角平分线.(2)了解三角形的三条高、三条中线与三条角平分线分别交于一点.2.难点:(1)三角形平分线与角平分线的区别,三角形的高与垂线的区别.(2)钝角三角形高的画法.(3)不同的三角形三条高的位置关系.【课时安排】1课时教学设计课前延伸一、课前预习:1.指导学生阅读课本P65-66.2.回答下面问题.(1)什么叫三角形的高?三角形的高与垂线有何区别和联系?三角形的高是从三角形的一个顶点向它对边所在的直线作垂线,顶点和垂足之间的线段,而从三角形一个顶点向它对边所在的直线作垂线这条垂线是直线.(2)什么叫三角形的中线?连结两点的线段与过两点的直线有何区别和联系?三角形的中线是连结一个顶点和它对边的中点的线段,而过两点的直线有着本质的不同,一个代表的是线段,另一个却是直线.(3)什么叫三角形的角平分线?三角形的角平分线与角平分线有何区别和联系?三角形的角平分线是三角形的一个内角平分线与它的对边相交,这个角顶点与交点之间的线段,而角平分线指的是一条射线.3.三角形的高、中线和角平分线是代表线段还是代表射线或直线?三角形的高、中线和角平分线都代表线段,这些线段的一个端点是三角形的一个顶点,另一个端点在这个顶点的对边上.二、检测预习情况:观察下列表中,回答预习问题:把下面图表投影出来:三角形的重要线段意义图形表示法三角形的高线从三角形的一个顶点向它的对边所在的直线作...