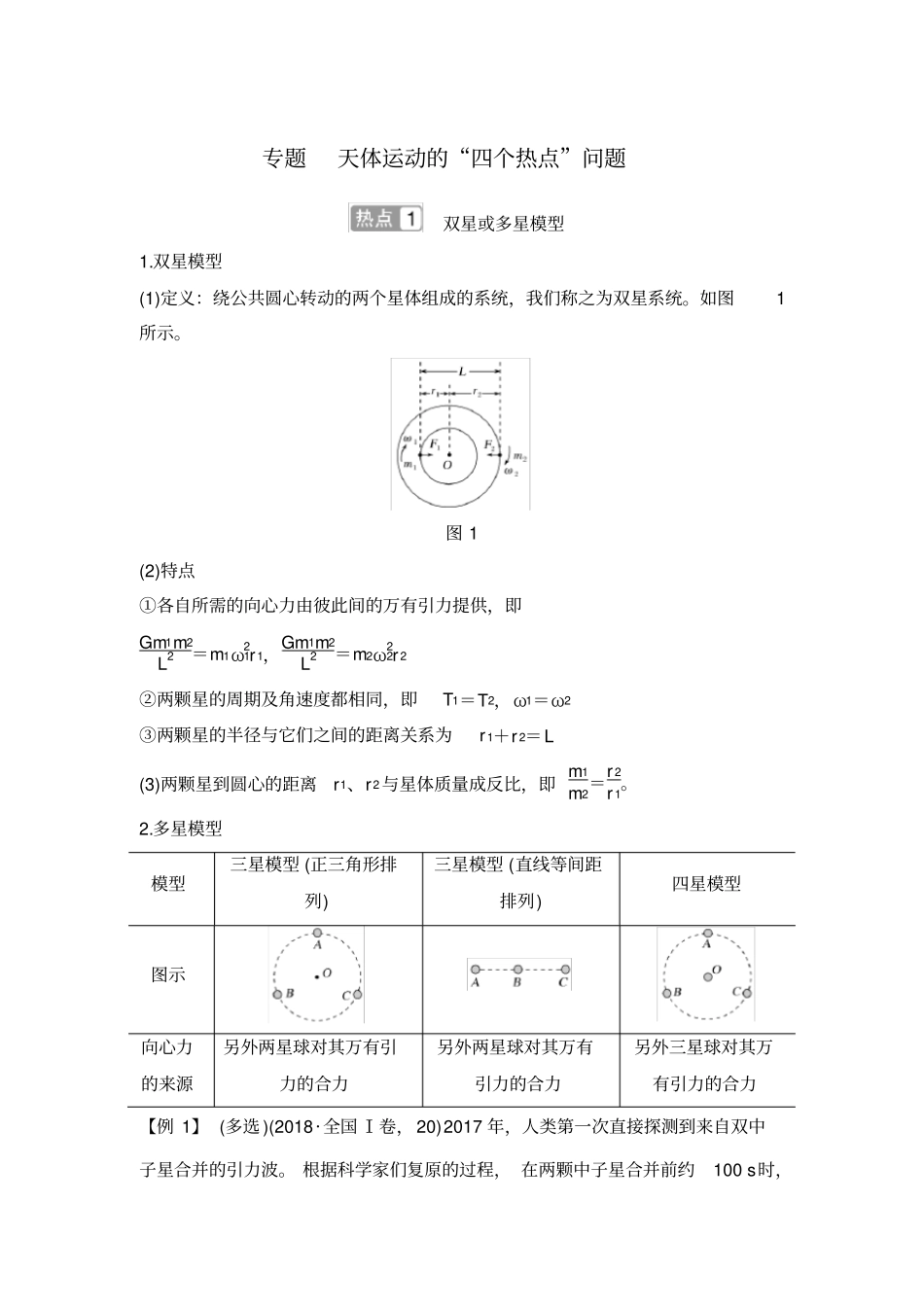
专题天体运动的“四个热点”问题双星或多星模型1.双星模型(1)定义:绕公共圆心转动的两个星体组成的系统,我们称之为双星系统。如图1所示。图1(2)特点①各自所需的向心力由彼此间的万有引力提供,即Gm1m2L2=m1ω21r1,Gm1m2L2=m2ω22r2②两颗星的周期及角速度都相同,即T1=T2,ω1=ω2③两颗星的半径与它们之间的距离关系为r1+r2=L(3)两颗星到圆心的距离r1、r2与星体质量成反比,即m1m2=r2r1。2.多星模型模型三星模型(正三角形排列)三星模型(直线等间距排列)四星模型图示向心力的来源另外两星球对其万有引力的合力另外两星球对其万有引力的合力另外三星球对其万有引力的合力【例1】(多选)(2018·全国Ⅰ卷,20)2017年,人类第一次直接探测到来自双中子星合并的引力波。根据科学家们复原的过程,在两颗中子星合并前约100s时,它们相距约400km,绕二者连线上的某点每秒转动12圈。将两颗中子星都看作是质量均匀分布的球体,由这些数据、万有引力常量并利用牛顿力学知识,可以估算出这一时刻两颗中子星()A.质量之积B.质量之和C.速率之和D.各自的自转角速度解析由题意可知,合并前两中子星绕连线上某点每秒转动12圈,则两中子星的周期相等,且均为T=112s,两中子星的角速度均为ω=2πT,两中子星构成了双星模型,假设两中子星的质量分别为m1、m2,轨道半径分别为r1、r2,速率分别为v1、v2,则有Gm1m2L2=m1ω2r1、Gm1m2L2=m2ω2r2,又r1+r2=L=400km,解得m1+m2=ω2L3G,A错误,B正确;又由v1=ωr1、v2=ωr2,则v1+v2=ω(r1+r2)=ωL,C正确;由题中的条件不能求解两中子星自转的角速度,D错误。答案BC1.(2019·吉林模拟)我国发射的“悟空”号暗物质粒子探测卫星,三年来对暗物质的观测研究已处于世界领先地位。宇宙空间中两颗质量相等的星球绕其连线中心匀速转动时,理论计算的周期与实际观测周期不符,且T理论T观测=k(k>1)。因此,科学家认为,在两星球之间存在暗物质。假设以两星球球心连线为直径的球体空间中均匀分布着暗物质(已知质量分布均匀的球体对外部质点的作用,等效于质量集中在球心处对质点的作用),两星球的质量均为m。那么暗物质的质量为()A.k2-28mB.k2-14mC.(k2-1)mD.(2k2-1)m解析双星均绕它们连线的中点做匀速圆周运动,令它们之间的距离为L,由万有引力提供向心力得Gm2L2=m4π2T2理论·L2,解得T理论=πL2LGm。根据观测结果,星体的运动周期T理论T观测=k,这种差异可能是由双星之间均匀分布的暗物质引起的,又均匀分布在球体内的暗物质对双星系统的作用与一质量等于球内暗物质的总质量m′(位于球心处)的质点对双星系统的作用相同,有Gm2L2+Gmm′(L2)2=m4π2T2观测·L2,解得T观测=πL2LG(m+4m′),所以m′=k2-14m。选项B正确。答案B2.(多选)为探测引力波,中山大学领衔的“天琴计划”将向太空发射三颗完全相同的卫星(SC1、SC2、SC3)构成一个等边三角形阵列,地球恰处于三角形的中心,卫星将在以地球为中心、离地面高度约10万公里的轨道上运行,针对确定的引力波源进行引力波探测。如图2所示,这三颗卫星在太空中的分列图类似乐器竖琴,故命名为“天琴计划”。已知地球同步卫星距离地面的高度约为3.6万公里,以下说法正确的是()图2A.若知道引力常量G及三颗卫星绕地球的运动周期T,则可估算出地球的密度B.三颗卫星具有相同大小的加速度C.三颗卫星绕地球运动的周期一定大于地球的自转周期D.从每颗卫星可以观察到地球上大于13的表面解析若知道引力常量G及三颗卫星绕地球的运动周期T根据万有引力提供向心力GMmr2=m4π2T2r,得到M=4π2r3GT2,因地球的半径未知,也不能计算出轨道半径r,不能计算出地球体积,故不能估算出地球的密度,选项A错误;根据GMmr2=ma,由于三颗卫星到地球的距离相等,则绕地球运动的轨道半径r相等,则它们的加速度大小相等,选项B正确;根据万有引力等于向心力,GMmr2=m4π2T2r解得T=2πr3GM,由于三颗卫星的轨道半径大于地球同步卫星的轨道半径,故三颗卫星绕地球运动的周期大于地球同步卫星绕地球运动的周期,即大于地球的自转周期,选项C正确;当等边三角形边与地球表面相切的时候,恰好看到地球表面...