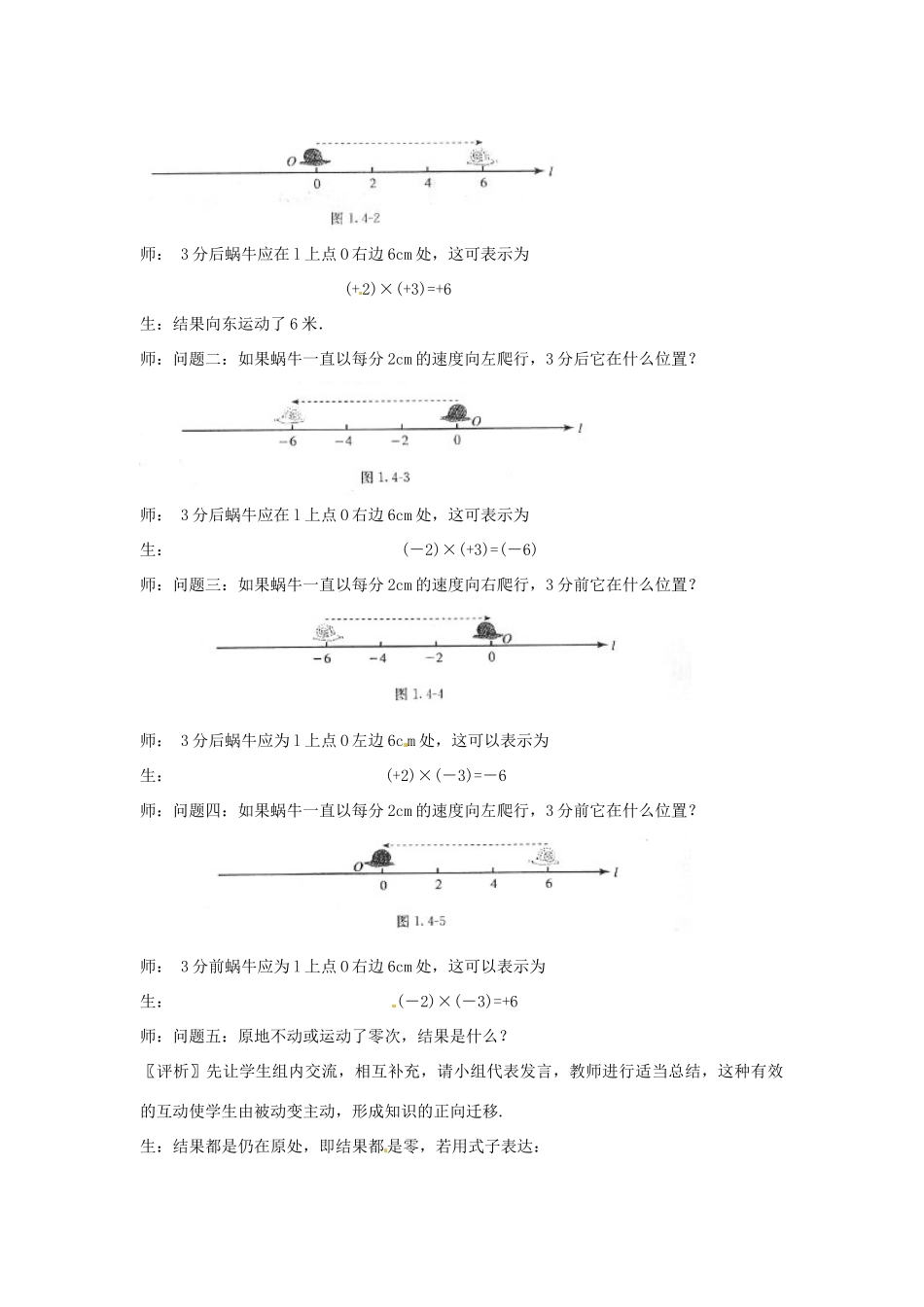
1.4.1有理数的乘法(1)【情境导入】师:前面我们已经学习了有理数的加法运算和减法运算,今天,我们开始研究有理数的乘法运算.问题一:有理数包括哪些数?生:有理数包括正整数、正分数、负整数、负分数和零.师:问题二:小学已经学过的乘法运算,属于有理数中哪些数的运算?生1:属于正有理数和零的乘法运算.生2:属于正整数、正分数和零的乘法运算.师:计算下列各题:(1)3×2;(2)3×;(3)×;(4)2×;(5)2×0;(6)0×.(学生板演)师:以上这些题,都是对正有理数与正有理数、正有理数与零、零与零的乘法,方法与小学学过的相同,今天我们要研究的有理数的乘法运算,重点就是要解决引入负有理数之后怎样进行乘法运算的问题.【探索新知】师:我们以蜗牛爬行距离为例,为区分方向,我们规定:向左为负,向右为正,为区分时间,我们规定:现在前为负,现在后为正.如图,一只蜗牛沿直线l爬行,它现在的位置恰在l上的点O.问题一:如果蜗牛一直以每分2cm的速度向右爬行,3分后它在什么位置?师:3分后蜗牛应在l上点O右边6cm处,这可表示为(+2)×(+3)=+6生:结果向东运动了6米.师:问题二:如果蜗牛一直以每分2cm的速度向左爬行,3分后它在什么位置?师:3分后蜗牛应在l上点O右边6cm处,这可表示为生:(-2)×(+3)=(-6)师:问题三:如果蜗牛一直以每分2cm的速度向右爬行,3分前它在什么位置?师:3分后蜗牛应为l上点O左边6cm处,这可以表示为生:(+2)×(-3)=-6师:问题四:如果蜗牛一直以每分2cm的速度向左爬行,3分前它在什么位置?师:3分前蜗牛应为l上点O右边6cm处,这可以表示为生:(-2)×(-3)=+6师:问题五:原地不动或运动了零次,结果是什么?〖评析〗先让学生组内交流,相互补充,请小组代表发言,教师进行适当总结,这种有效的互动使学生由被动变主动,形成知识的正向迁移.生:结果都是仍在原处,即结果都是零,若用式子表达:0×3=0;0×(-3)=0;2×0=0;(-2)×0=0.师:综合上述五个问题得出:(1)(+2)×(+3)=+6;(2)(-2)×(+3)=-6;(3)(+2)×(-3)=-6;(4)(-2)×(-3)=+6.(5)任何数与零相乘都得零.师:观察上述(1)~(4)回答:1.积的符号与因数的符号有什么关系?2.积的绝对值与因数的绝对值有什么关系?生:1.若两个因数的符号相同,则积的符号为正;若两个因数的符号相反,则积的符号为负.2.积的绝对值等于两个因数的绝对值的积.师:由此我们可以得到:两数相乘,同号得正,异号得负,并把绝对值相乘.〖评析〗充分利用了数形结合的教学手段,激发学生探究新知的兴趣.设计意图是让学生体验数学与现实生活有密切联系,使数学学习发生在真实的世界和背景中,提高学生学习数学的兴趣和参与程度,同时为学生研究乘法法则创设探索的情境.【形成新知】师:思考一下这些问题.正数乘正数积为数.负数乘正数积为数.正数乘负数积为数.负数乘负数积为数.乘积的绝对值等于各乘数绝对值的.同学们踊跃回答.师:有理数的乘法法则是什么?学生总结两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.师:例1计算(-3)×9;(2)(-)×2.生:-27,-1.说明:乘积是1的两个数互为倒数.师:用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km气温的变化量为-60C,攀登3km后,气温有什么变化?师:观察:下列各式的积是正的还是负的?2×3×4×(-5),2×3×(-4)×(-5),2×(×3)×(×4)×(-5),(-2)×(-3)×0×(-5).〖评析〗归纳特点,引出法则。提出0为因数的两种情况,板书出算式,并分类探究,观察,励学生多观察,多动脑,针对学生学习的难点,疑点进行释疑.在学生充分发表意见的基础上,总结出有理数的乘法法则.设计意图是培养观察能力、概括能力,感受归纳方法和化归思想.思考:几个不是0的数相乘,积的符号与负因数的个数之间有什么关系?生:分组讨论交流,再用自己的语言表达所发现的规律:几个不是0的数相乘,负因数的个数是时,积是正数;负因数的个数是时,积是负数.师:例3计算:(1)(-3)×(-)×(-),(2)(-5)×6×(-)×.解题步骤:1.认清题目...