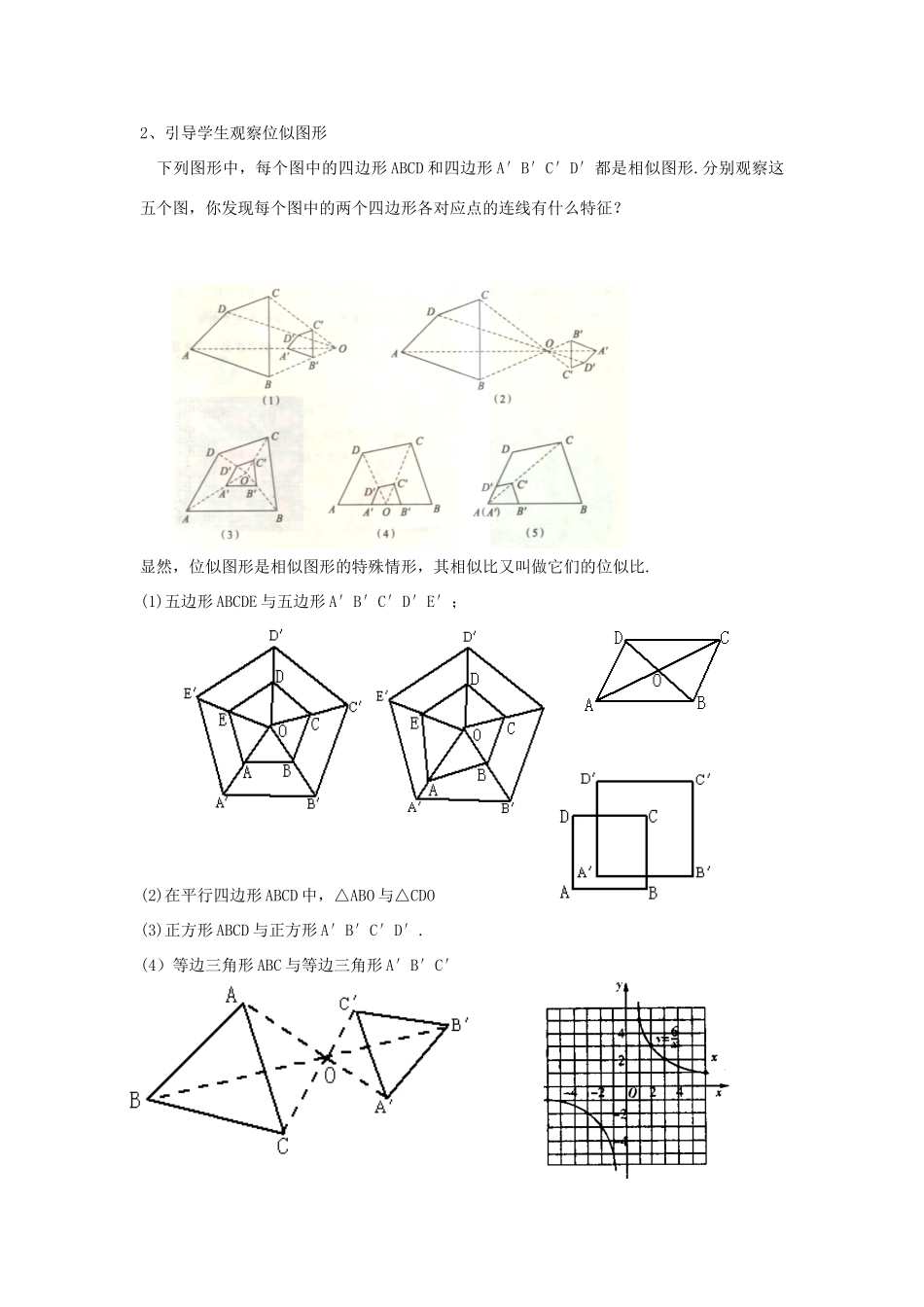
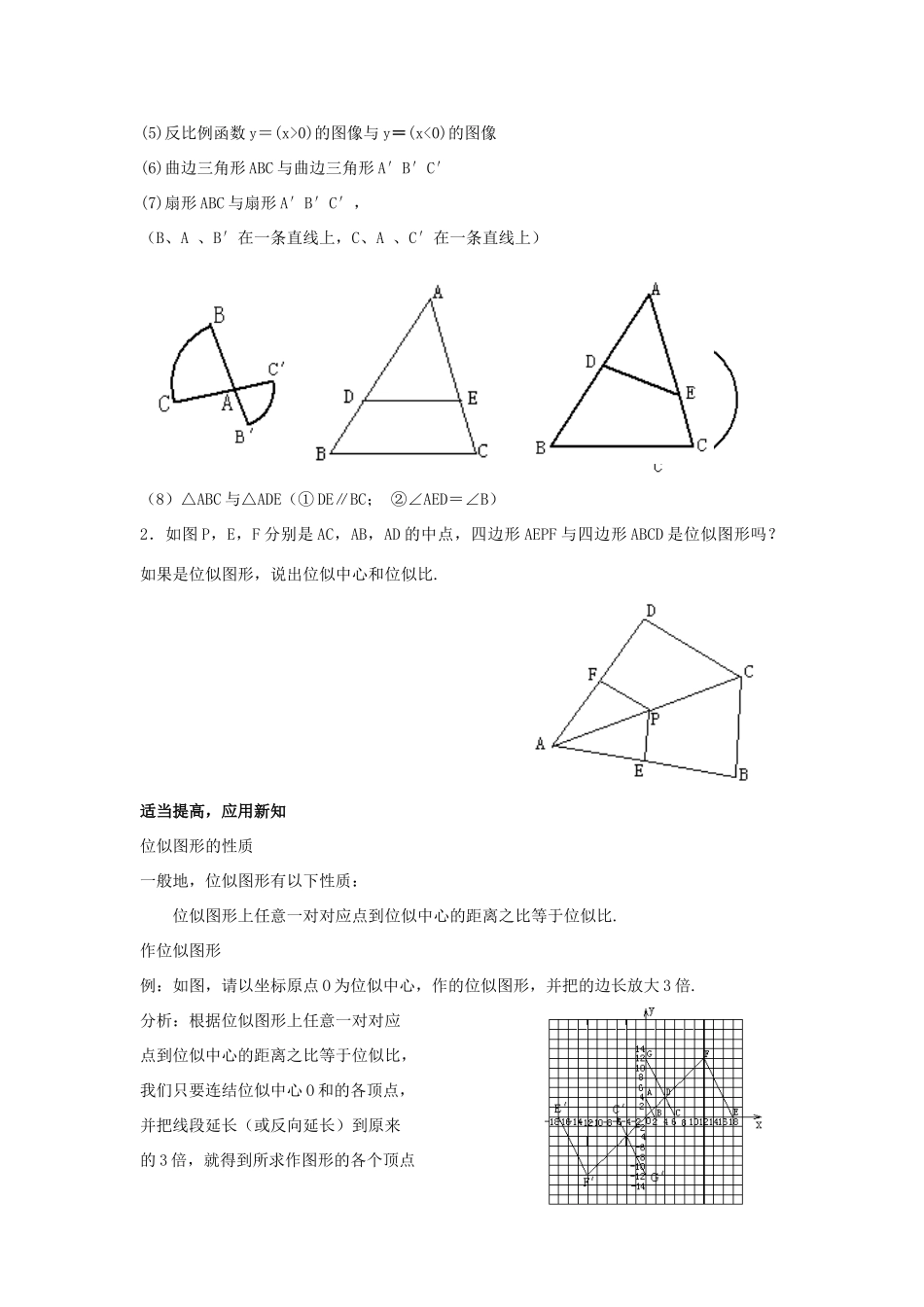
湖南省宁乡县三仙坳初级中学九年级数学下册《27.3位似(第三课时)》教案新人教版第三课时教学目标:(一)知识与技能1.进一步理解图形的位似概念,掌握位似图形的性质。2.会利用作位似图形的方法把一个图形进行放大或缩小。3.掌握直角坐标系中图形的位似变化与对应点坐标变化的规律。(二)过程与方法1、经历位似图形性质的探索过程,进一步发展学生的探究、交流能力、以及动手、动脑、手脑和谐一致的习惯。2、利用图形的位似解决一些简单的实际问题,并在此过程中培养学生的数学应用意识,进一步培养学生动手操作的良好习惯。(三)情感态度与价值观通过动手操作、探究与交流,发展学生的合情推理能力和初步的逻辑推理能力。教学重点和难点:本节教学的重点是图形的位似概念、位似图形的性质及利用位似把一个图形放大或缩小。教学过程:创设情景,构建新知1.位似图形的概念下列两幅图有什么共同特点?如果两个图形不仅形状相同,而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.2、引导学生观察位似图形下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.(1)五边形ABCDE与五边形A′B′C′D′E′;(2)在平行四边形ABCD中,△ABO与△CDO(3)正方形ABCD与正方形A′B′C′D′.(4)等边三角形ABC与等边三角形A′B′C′(5)反比例函数y=(x>0)的图像与y=(x<0)的图像(6)曲边三角形ABC与曲边三角形A′B′C′(7)扇形ABC与扇形A′B′C′,(B、A、B′在一条直线上,C、A、C′在一条直线上)(8)△ABC与△ADE(①DE∥BC;②∠AED=∠B)2.如图P,E,F分别是AC,AB,AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比.适当提高,应用新知位似图形的性质一般地,位似图形有以下性质:位似图形上任意一对对应点到位似中心的距离之比等于位似比.作位似图形例:如图,请以坐标原点O为位似中心,作的位似图形,并把的边长放大3倍.分析:根据位似图形上任意一对对应点到位似中心的距离之比等于位似比,我们只要连结位似中心O和的各顶点,并把线段延长(或反向延长)到原来的3倍,就得到所求作图形的各个顶点直角坐标系中图形的位似变化与对应点坐标变化的规律想一想:1.四边形GCEF与四边形G′C′E′F′具有怎样的对称性?2.怎样运用像与原像对应点的坐标关系,画出以原点为位似中心的位似图形?以坐标原点为位似中心的位似变换有一下性质:若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为(kx,ky)或(―kx,―ky).练一练1.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长缩小到原来的一半.2.如图,在直角坐标系中,△ABC的各个坐标为A(-1,1),B(2,3),C(0,3)。现要以坐标原点0为位似中心,位似比为,作△ABC的位似图形△A/B/C/,则它的顶点A、B、C的坐标各是多少?小结内容,自我反馈今天你学会了什么?位似图形的定义,位似图形的性质.作业1.P65习题27.31、2、3配套课时练习1.位似这种变换是将图形的_________改变,而保持图形的________不变。2.如图所示,四边形ACDE∽四边形ABHF,则它们的位似中心是____________。3.如图所示,点D、点E分别是AB、AC边中点,则△_________∽△_______,它们的位似中心是___________,相似比是__________。4.如图所示中位似的图形是__________(填序号)。5.已知四边形ABCD,如图所示。画一个四边形,使四边形与原图形的相似比为2.5。6.请用位似的方法把下图放大1倍,要求位似中心在AB边上。7.玩一玩挡光板:小明学了“位似变换”以后,周末在家做了一个“位似”小实验(如图所示),为了使家中的墙壁上一幅壁画不受太阳光从点O照射,他在壁画与入射光线O之间设置一个长方形障碍,以拦住壁画不受照射,要求使壁画和障碍物成位似图形,相似比为3:1,请你帮小明画出其位似图形。8.如图所示,按要求进行位似变换:(1)将△ABC放大2倍,且位似...