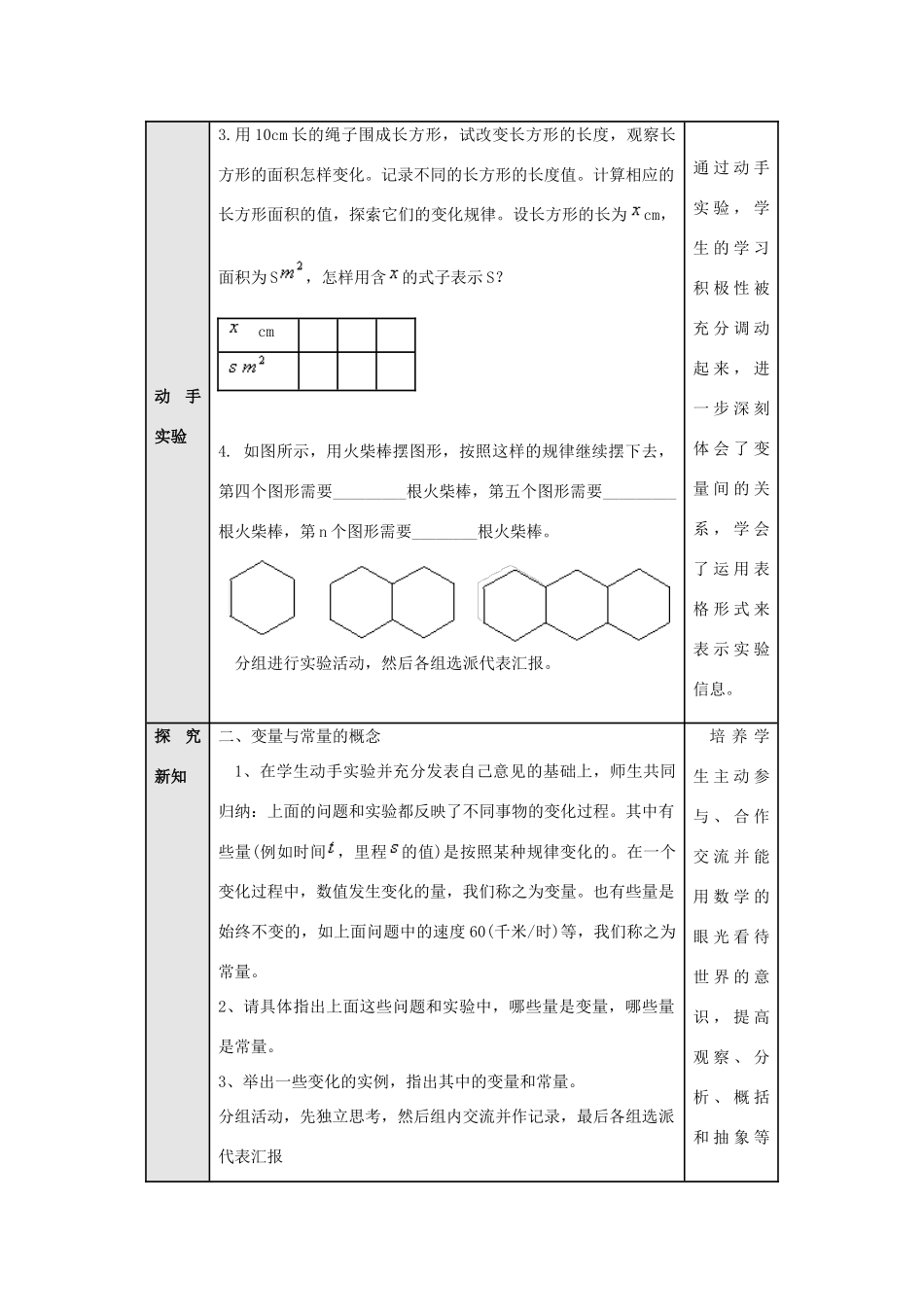
“变量与函数”教学设计教学目标1、运用丰富的实例,使学生在具体情境中领悟函数概念的意义,了解常量与变量的含义,能分清实例中的常量与变量,了解自变量与函数的意义。2、通过动手实践与探索,让学生参与变量的发现和函数概念的形成过程,以提高分析问题和解决问题的能力。3、引导学生探索实际问题中的数量关系,培养对学习的兴趣和积极参与数学活动的热情。在解决问题的过程中体会数学的应用价值并感受成功的喜悦,建立自信心。教学难点函数概念的形成过程知识重点正确理解函数的概念教学过程(师生活动)设计理念创设情境提出问题一、引入1、汽车以60千米/时的速度匀速行驶,行驶里程为千米,行驶时间为小时,先填写下表,再试着用含的式子表示。(小时)12345(千米)2、要画一个面积S为10的圆,圆的半径应取多少?圆面积为呢?怎样用含圆面积S的式子表示圆半径?让学生充分发表意见,然后教师点评。挖掘和利用实际生活中与变量有关的问题情景,让学生经历探索具体情景中两个变量关系的过程,直接获得探索变量关系的体验。动手实验3.用10cm长的绳子围成长方形,试改变长方形的长度,观察长方形的面积怎样变化。记录不同的长方形的长度值。计算相应的长方形面积的值,探索它们的变化规律。设长方形的长为cm,面积为S,怎样用含的式子表示S?4.如图所示,用火柴棒摆图形,按照这样的规律继续摆下去,第四个图形需要_________根火柴棒,第五个图形需要_________根火柴棒,第n个图形需要________根火柴棒。分组进行实验活动,然后各组选派代表汇报。通过动手实验,学生的学习积极性被充分调动起来,进一步深刻体会了变量间的关系,学会了运用表格形式来表示实验信息。探究新知二、变量与常量的概念1、在学生动手实验并充分发表自己意见的基础上,师生共同归纳:上面的问题和实验都反映了不同事物的变化过程。其中有些量(例如时间,里程的值)是按照某种规律变化的。在一个变化过程中,数值发生变化的量,我们称之为变量。也有些量是始终不变的,如上面问题中的速度60(千米/时)等,我们称之为常量。2、请具体指出上面这些问题和实验中,哪些量是变量,哪些量是常量。3、举出一些变化的实例,指出其中的变量和常量。分组活动,先独立思考,然后组内交流并作记录,最后各组选派代表汇报培养学生主动参与、合作交流并能用数学的眼光看待世界的意识,提高观察、分析、概括和抽象等cm三、函数的概念1、在前面的每个问题和实验中,是否各有两个变量?同一个问题中的变量之间有什么联系?师生分析得出:上面的每个问题和实验中的两个变量互相联系。当其中一个变量取定一个值时,另一个变量就有惟一确定的值。1、一般来说,在一个变化过程中,如果有两个变量与,并且对于的每一个确定的值,都有惟一确定的值与其对应,那么我们就说是自变量,是的函数。如果当时,那么叫做当自变量的值为时的函数值。例如在问题1中,时间是自变量,里程是的函数。时,其函数值为60,时,其函数值为120。四、例题1、一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量(单位:L)随行驶里程(单位:km)的增加而减少,平均耗油量为0.1L/km。问题1:写出表示与的函数关系的式子。问题2:指出自变量的取值范围。问题3:汽车行驶200km时,油箱中还有多少汽油?学生分组讨论、交流、说出各自得到的结论,最后师生共同归纳,得出⑴与的函数关系式是⑵自变量的取值范围是0≤≤500。⑶汽车行驶200km时,油箱中还有30L汽油。教师提示:确定自变量的取值范围时,不仅要考虑到函数关系式的能力。必须有意义,而且还要注意问题的实际意义。2.一个小球由静止开始在一个斜坡上向下滚动,其速度每秒增加2m。(1)在这一变化过程中反映了哪两个变量之间的关系?它们之间可建立怎样的函数关系?(2)4.5秒时小球的速度为多少?巩固练习1.说出下列公式中的常量和变量(1)设圆的半径为R,周长为C,则,其中常量为_____,变量为______(2)球的表面积S与球半径R的关系式为,其中常量为_____,变量为______2.在△ABC中,设它的底边是a,底边上的高是h,则三角形的面积为,指出下列各式中的常量和变量:(1)S=6h,常量为____...