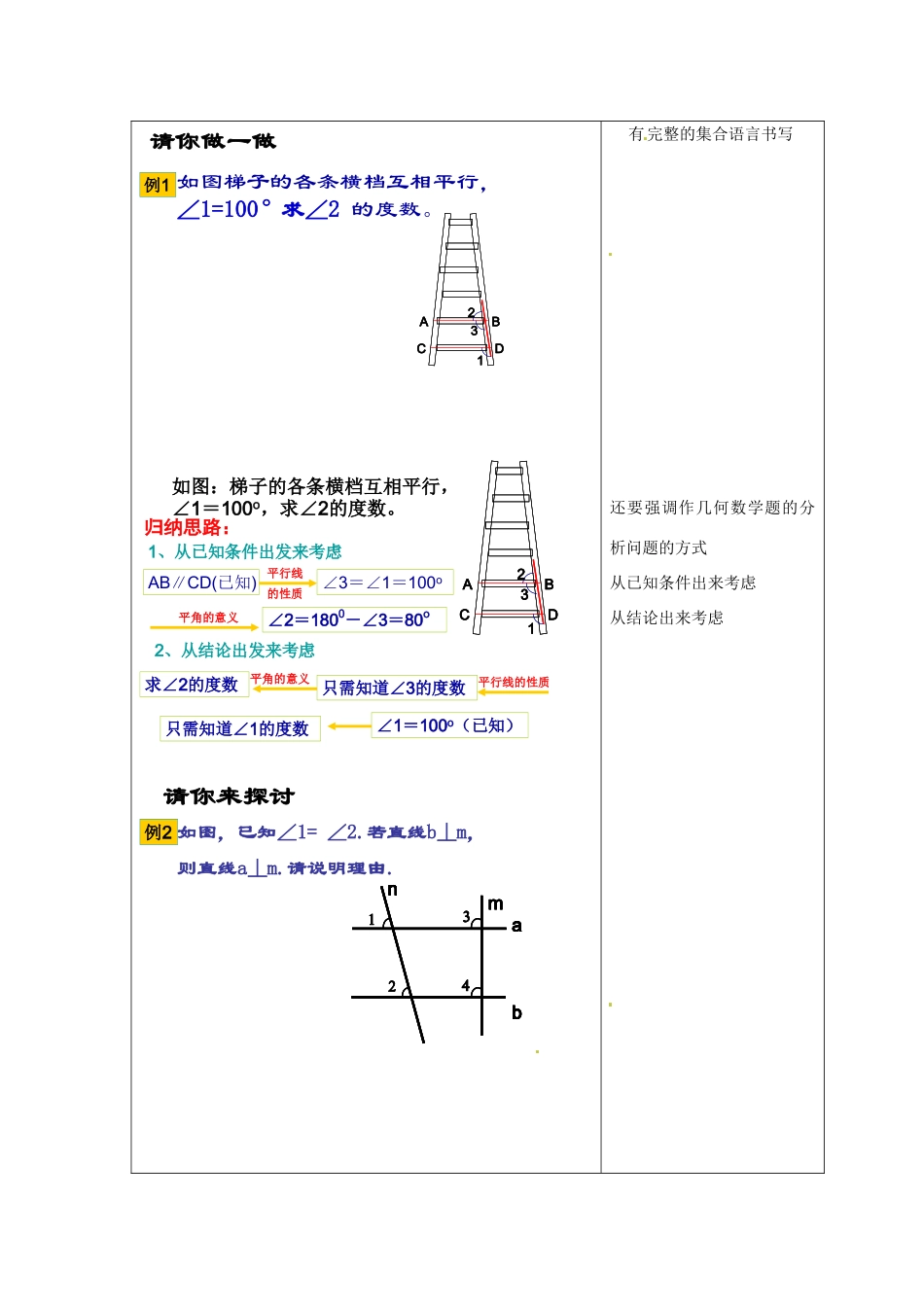
平行线的性质(第1课时)教学目标知识目标:平行线的性质与平行线的判定是相反问题,平行线的性质,会用平行线的性质进行推理和计算.能力目标:1.通过画平行线、度量角培养学生实际操作能力(即画图测量的能力).2.通过平行线性质定理的推导,培养学生的观察分析和进行简单的逻辑推理能力.情感目标:通过学习平行线的性质与判定的联系与区别,培养学生事物是普遍联系又是相互区别的辩证唯物主义思想.教学重点平行线的性质公理及平行线性质定理的推理.教学难点平行线性质与判定的区别及推理过程.教学过程(1)用直尺和三角尺画出两条平行线a∥b,再画一条截线c,使之与直线a,b相交,并标出所形成的八个角.我们一起来动手(2)测量上面八个角的大小,记录下来.ababc从中你能发现什么?(3)图中哪些角是同位角,它们具有怎么的数量关系?设计意图温故知新,引入新课两条平行线被第三条直线所截,同位角相等。简单地说:两直线平行,同位角相等。ABCD12ABCDABCD12∵AB//CD∴∠∠1=1=∠∠22几何语言:(两直线平行,同位角相等)请你来说一说判定定理和性质定理有什么区别?同位角相等同位角相等两直线平行两直线平行两直线平行两直线平行同位角相等同位角相等条件条件结论结论条件条件结论结论判定定理性质定理条件条件结论结论条件条件结论结论判定定理性质定理判定定理性质定理发现:二者条件与结论正好相反由“线”定“角”由“线”的位置关系(平行)定“角”的数量关系(相等)由“角”定“线”由“角”的数量关系(相等)定“线”的位置关系(平行)性质定理判定定理通过合作学习,自主学习发现新知联系判定定理进行区别例1,2作为课堂练习巩固新知,特别是要求学生要请你做一做如图梯子的各条横档互相平行,∠1=100°求∠2的度数。例112ABCD312ABCD3如图:梯子的各条横档互相平行,∠1=100o,求∠2的度数。12ABCD312ABCD3归纳思路:1、从已知条件出发来考虑AB∥CD(已知)∠3=∠1=100o∠2=1800-∠3=80o平行线的性质平角的意义2、从结论出发来考虑求∠2的度数只需知道∠3的度数只需知道∠1的度数∠1=100o(已知)平角的意义平行线的性质如图,已知∠1=∠2.若直线b⊥m,则直线a⊥m.请说明理由.请你来探讨abmn1234abmnabmnabmn1234例2有完整的集合语言书写还要强调作几何数学题的分析问题的方式从已知条件出来考虑从结论出来考虑cdab3421cdab3421cdab3421ab3421如图所示∠∠3=3=∠∠44求证求证::∠∠1=1=∠∠22请你来完成巩固知识辨析真伪作业布置:常规三项