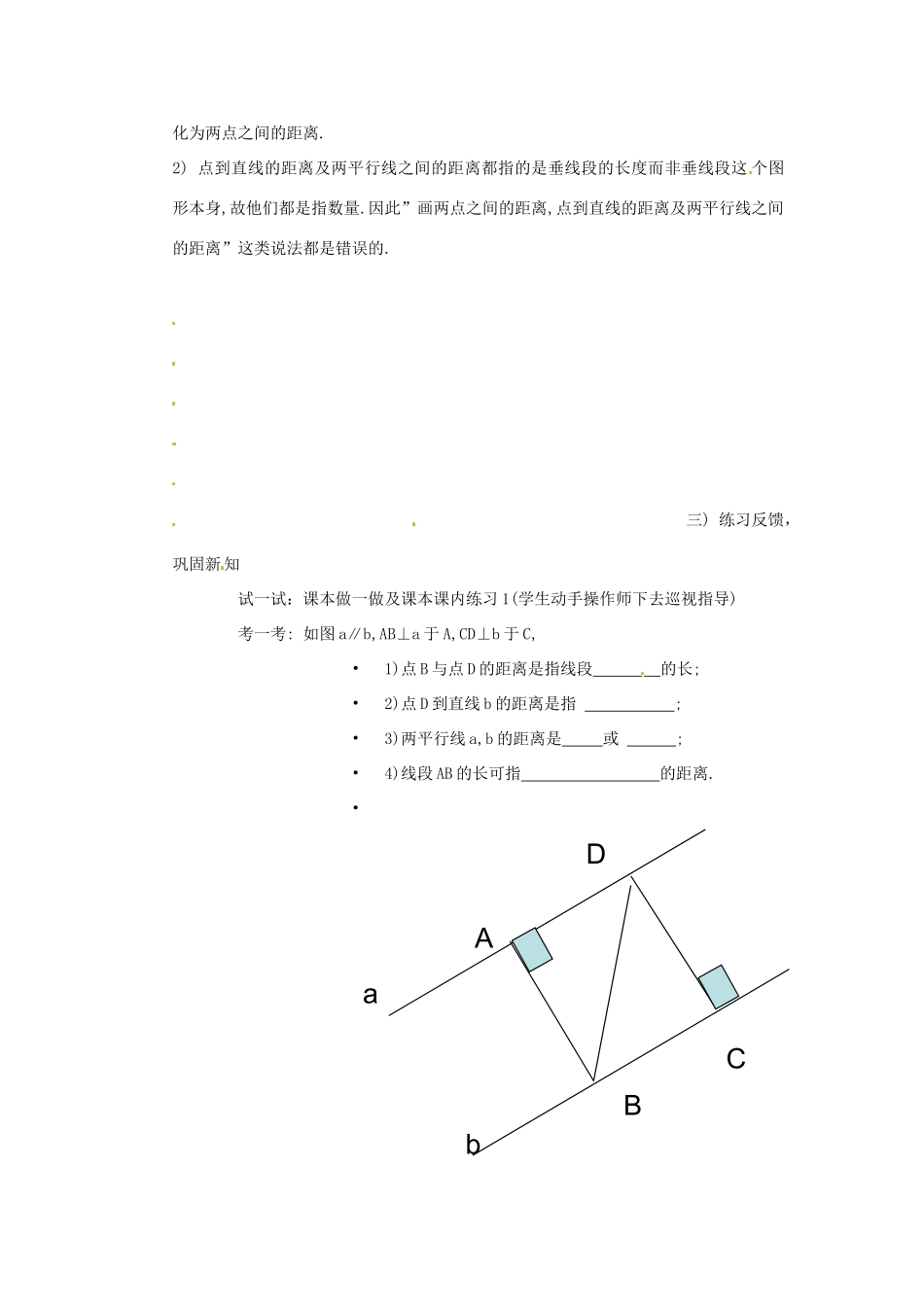
平行线之间的距离一.教学目标知识与技能目标:1。理解两条平行线之间的距离的概念过程与方法目标:1。体会两条平行线之间的距离的意义情感与态度目标:1。学会度量两条平行线之间的距离及平移已知直线,使所得的像与已知直线的距离等于已知长.2.让学生在合作学习,直观探究中探索归纳两条平行线之间的距离二)师生互动,讲授新课1.合作学习学生动手操作:任意画两条互相平行的直线a和b1)在直线a上,任意取两点A,B,分别作AC⊥b于点C,BD⊥b于点D.量出线段AC,BD的长度,你有何发现?2)如果把一把三角尺的一条直角边沿着直线b移动,观察三角尺的另一条直角边与直线a交点处的刻度,你又有何发现?2.经合作学习归纳得到:两条平行线中,一条直线上的点到另一条直线的距离处处相等.3.师指出:在数学上这个距离就叫做这两平行线之间的距离.比如上述中,线段AC,BD的长度相等,它就是两平行线a和b之间的距离.4.类比三概念:1)点到直线的距离及两平行线之间的距离两者实际上都是两点间的距离.前者其中一点是已知点,另一点是过已知点作已知直线的垂线时的垂足;而后者其中一点是一直线上的任意一点,另一点是过该点过作另一直线的垂线时的垂足.所以几何中的距离都是转化为两点之间的距离.2)点到直线的距离及两平行线之间的距离都指的是垂线段的长度而非垂线段这个图形本身,故他们都是指数量.因此”画两点之间的距离,点到直线的距离及两平行线之间的距离”这类说法都是错误的.三)练习反馈,巩固新知试一试:课本做一做及课本课内练习1(学生动手操作师下去巡视指导)考一考:如图a∥b,AB⊥a于A,CD⊥b于C,•1)点B与点D的距离是指线段的长;•2)点D到直线b的距离是指;•3)两平行线a,b的距离是或;•4)线段AB的长可指的距离.•AbaDCB例题分析:已知直线l,把这条直线平移,使经平移所得的像与直线l的距离为1.5cm,求作直线l平移后所得的像.思路分析:本题是求经平移变换后所得的像,因此切入点应引导学生回顾平移变换的两要素(平移方向和距离)及转化思想(作点的平移变换的像是图形平移变换作图的基本方法)做法说明:要注意说明课本做法4的多种操作方法结论处理:只要找到能满足题意的一个即可思维发散:1)针对题中方向的不确定性讨论”能作出几条符合要求的直线”2)将原图中的已知直线位置方向和距离进行改变,再次进行求解.巩固一练:课本课内练习2(学生口答并要求量出正确的距离)四)梳理知识,总结收获(鼓励学生归纳知识)1)用类比思想掌握三概念2)学会度量两条平行线之间的距离及平移已知直线,使所得的像与已知直线的距离等于已知长.五)布置作业:l