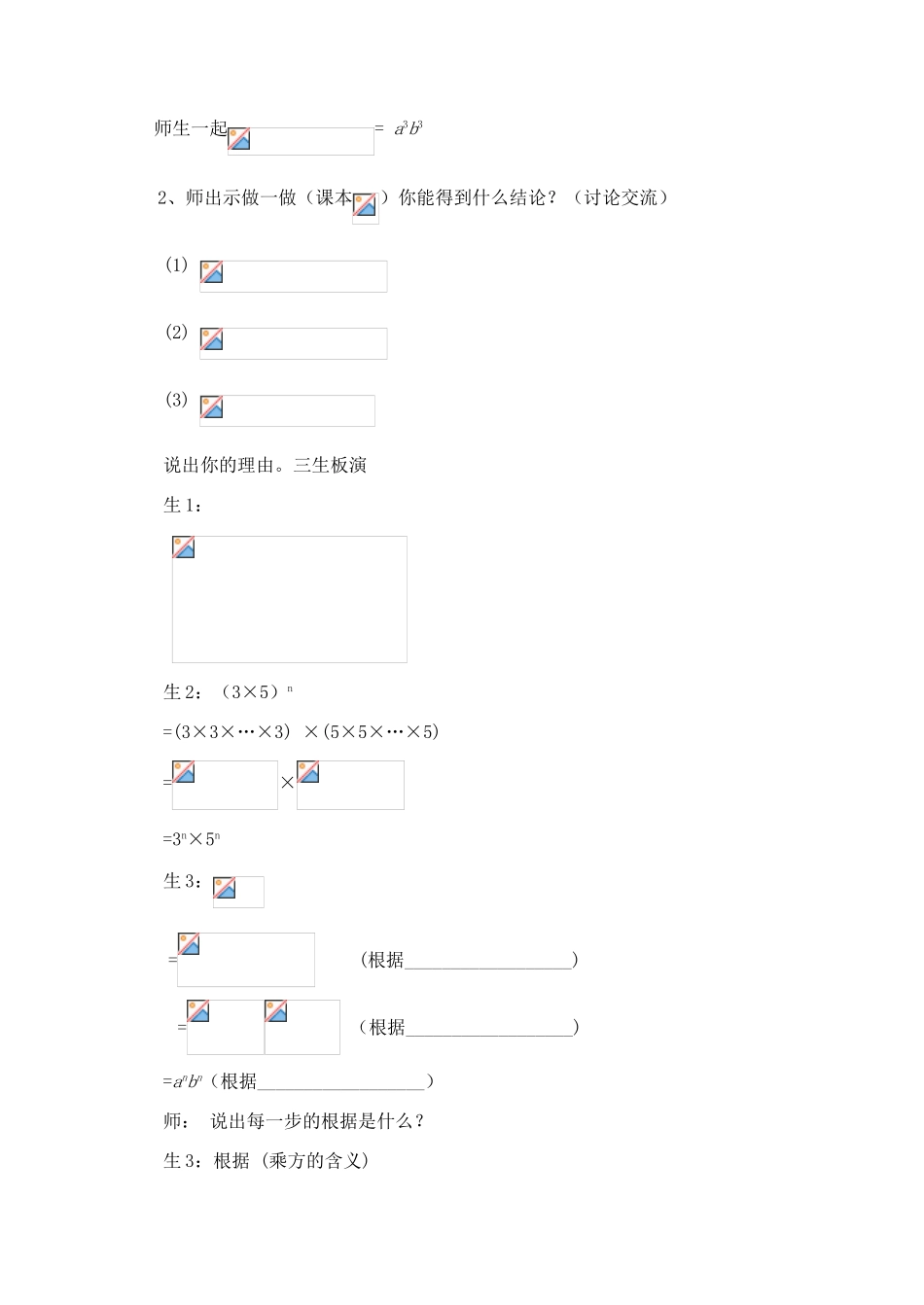
山东省枣庄市峄城区吴林街道中学七年级数学下册《第一章,幂的乘方与积的乘方》教案2(新版)北师大版教学目标1.使学生理解并掌握积的乘方法则.2.使学生能灵活地运用积的乘方法则进行计算.3.通过法则的推导过程培养学生分析问题、解决问题的能力.教学重点和难点重点:法则的理解与掌握.难点:法则的灵活运用.教法及学法指导:以学生活动为主线,通过精心设计的问题导语启发、点拨,引导学生观察、探究、讨论、对比、归纳、发现、创造等参与活动的综合形式教学.在学习过程中,给学生足够的合作交流空间,加深对法则的探索过程及对算理的理解,指导学生在课堂实践活动中,自主探索,合作交流,获得知识,提高技能,培养创造意识.课前准备:多媒体课件教学过程一、复习回顾从学生原有认知结构提出问题(一)学生默写有关幂的三个知识点:1.幂的意义:2.同底数幂的乘法运算法则(m、n为正整数)3.幂的乘方运算法则((aamm))nn==aamnmn((mm、、nn都是正整数都是正整数))4.用文字叙述同底数幂乘法法则与幂的乘方法则.(二)判断正误:(1);(2);(3);(4);(5);(6);(7)设计意图:幂的意义在本节课中仍旧是法则推导的主要依据,其地位不可小觑,而同底数幂的乘法的推导过程,其中包含的算理知识在本堂课中仍是精神主旨,判断题与计算题相比更能考查学生分析问题、解决问题的能力。二、创设情境引入新课师出示引例:地球可以近似地看做是球体,如果用V,r分别代表球的体积和半半径,那么..地球的半径约为6×103km,它的体积大约是多少立方千米?生:列式..师:师:怎样计算呢?你能给这个式子起个名吗?师:进一步引导是6与103的什么运算?生:是6与103的乘积.师:类似于的运算就是积的乘方(板书课题1.2幂的乘方的积的乘方(二)).设计意图:从问题情境开始引起学生兴趣,好奇心.激发求知欲.在探索的过程中学生很自然地体会到学习积的乘方运算的必要性,了解数学与现实世界的联系.三、小组合作探究新知师:引导学生得到积的乘方法则1、师:根据幂的意义,(ab)3表示什么?生:ab·ab·ab,师:能否应用乘法的交换律和结合律.把它写成其它什么形式?师生一起=a3b32、师出示做一做(课本)你能得到什么结论?(讨论交流)(1)(2)(3)说出你的理由。三生板演生1:生2:(3×5)n=(3×3×…×3)×(5×5×…×5)=×=3n×5n生3:=(根据__________________)=(根据__________________)=anbn(根据__________________)师:说出每一步的根据是什么?生3:根据(乘方的含义)根据(交换律、结合律)根据(乘方的含义)师:于是我们得到了积的乘方法则:(ab)=(n是正整数).你试着用语言描述这个法则.生:(讨论、交流、然后总结:)生4:积的乘方等于积的每个因式分别乘方,再把所得的幂相乘.生5:积的乘方也就是集中的每个因数乘方,再相乘.生6:简单地说:积的乘方等于乘方的积.师:引导学生剖析积的乘方法则(1)形式是积的乘方;(2)结论积中各因数分别乘方,再相乘。师:如果是多个因式的积呢?(abc)n=?生:猜测、探究(abc)n=anbncn师生共同总结:三个或三个以上的积的乘方,也具有这一性质.设计意图:在得到法则时先鼓励学生进行猜想结果,然后再来验证这样的一个字母表达的过程.探索的方式从特殊到一般,符合学生的认知规律,进而总结出积的乘方的法则.由特殊的例子的探讨,引导到一般规律的发现,这几乎是数学的“创造学习”(即从学生的观点看是创造)的必由之路!通过再创造获得的知识与能力,要比以被动方式获得的,理解得更好,也更容易掌握.知识拓展也要把握时机.前一环节探索新知识本环节中提示用不同的方法证(abc)n=an·bn·cn,这本身在开拓学生思路方面也是一个促进.四、例题示范应用法则例1计算:(1)(3x)2;(2)(-2b)5;(3)(-2xy)4;(4)(3a2)n第(1)小题由学生回答,教师板演,并要求学生说出每一步的根据是什么;第(2)、(3)、(4)小题由学生板演,根据学生板演的情况,提醒学生注意:(1)系数的乘方;(2)因数中若有幂的形式,要注意运算要彻底。积的乘方积的乘方乘方的积乘方的积解:(1)(-3x)2=(-3)2·x2=9x2;生1:(2)(-2b)5=生2:(-2xy)4=(-2)4x4y4=16x4y4生3:(4)(3a2)n=3n(a2)n=3na2n第(1)...