一次函数的图象VIP免费

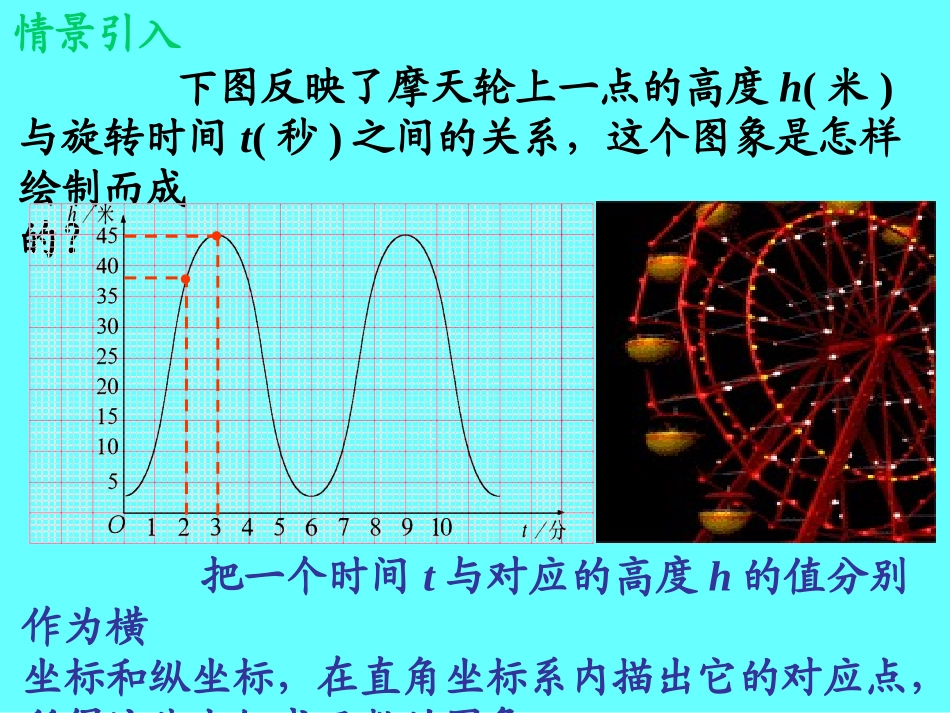
北师大版八年级(上)6.3一次函数的图象(1)6.3一次函数的图象(1)第六章一次函数西安市第六十二中学姚家健知识回顾1.若两个变量x,y间的关系式可以表示成_________(k,b为_____且k_____)形式,则称y是x的一次函数(x为_______,y为_______)特别地,当b=___时,称y是x的正比例函数.2、函数的表示方法：y=kx+b常数自变量因变量00图象法列表法解析法下图反映了摩天轮上一点的高度h(米)与旋转时间t(秒)之间的关系，这个图象是怎样绘制而成的？情景引入把一个时间t与对应的高度h的值分别作为横坐标和纵坐标，在直角坐标系内描出它的对应点，所得这些点组成函数的图象。新知归纳函数图象的定义：把一个函数的自变量x与对应的因变量y的值分别作为横坐标和纵坐标，在直角坐标系内描出它的对应点，所得这些点组成的图形叫做该函数的图象。例如：一次函数y＝kx＋b的图象叫一次函数图象,那正比例函数y＝kx呢？Ⅰ、作出一次函数的图象。12xyx…–2–1012…y…–3–1135…解：(1)列表新知探究自变量的值和函数的对应值具有代表性Ⅰ、作出一次函数的图象。12xyx…–2–1012…y…–3–1135…解：(1)列表yxO-5-4-3-2-11234554321-1-2-3-4-5(−2,−3)(−1,−1)(0,1)(1,3)(2,5)(2)描点新知探究将自变量的值和对应的函数值分别作为、纵坐标，在坐标系中描出表格中的各点；Ⅰ、作出一次函数的图象。12xyx…–2–1012…y…–3–1135…解：(1)列表(−2,−3)(1,3)yxO-5-4-3-2-11234554321-1-2-3-4-5(−1,−1)(0,1)(2,5)12xy(2)描点(3)连线新知探究按自变量从小到大的顺序，把所有点用平滑的曲线连接起来。新知归纳作函数图象的一般步骤：(1)列表：选择具有代表性的自变量的值和函数的对应值列成表格；(2)描点：将自变量的值作为横坐标，对应的函数值作为纵坐标，在坐标系中描出表格中的各点；(3)连线：按自变量从小到大的顺序，把所有点用平滑的曲线连接起来。Ⅱ、作出一次函数的图象，在图象上取几个点，找出它们的横坐标和纵坐标，并验证它们是否都满足关系式。52xy52xy(1)列表x…–10123…y…7531–1…(2)描点yO-5-4-3-2-1123457654321-1-2-3x(−1,7)(0,5)(1,3)(2,1)(3,−1)52xy(3)连线(4,−3)新知探究合作交流ⅰ、满足关系式的所有x、y所对应的点(x,y)都在一次函数的图象上吗？52xy52xyyO-5-4-3-2-1123457654321-1-2-3x(−1,7)(0,5)(1,3)(2,1)(3,−1)52xy满足函数关系式所有x、y对应的点(x,y)都在一次函数的图象上。合作交流yO-5-4-3-2-1123457654321-1-2-3x(−1,7)(0,5)(1,3)(2,1)(3,−1)52xyⅱ、一次函数的图象上的点(x,y)都满足关系式的吗？52xy52xy一次函数的图象上所有的点(x,y)都满足函数关系式。合作交流ⅲ、一次函数的图象有什么特点？bkxy1、一次函数的图象是一条直线,直线上的点与一次函数y=kx+b对应的x、y的值一一对应。3、两点确定一条直线2、一次函数y＝kx＋b的图象称为直线y＝kx＋b。新知归纳1、一次函数的图象：一次函数的图象是一条直线。直线上的点与一次函数y=kx+b对应的x、y的值一一对应。bkxy2、一次函数图象的画法：用两点法画一次函数的图象。bkxy1、一次函数的大致图象是()巩固练习32xyyxOyxyxOyxyxOyxyxOyxABCDB2、直线与x轴的交点坐标为，与y轴的交点坐标为。3、作出下列一次函数的图象：（1）y=−3x+1,(2)y=−x（3）y=2x−1，（4）y=3x巩固练习1xy(1.0)(0.1)补充知识yxOyxObkxy两点法(0,b)(,0)kb课堂小结:通过这堂课的学习，你知道了什么？1、了解函数图象的定义：2、作函数图象的一般步骤：列表、描点、连线。3、一次函数的图象：是一条直线。直线上的点与一次函数y=kx+b对应的x、y的值一一对应。4、一次函数图象的画法：两点法。bkxybkxy习题6.31、2课外练习：练习册132页1-3题作业作业