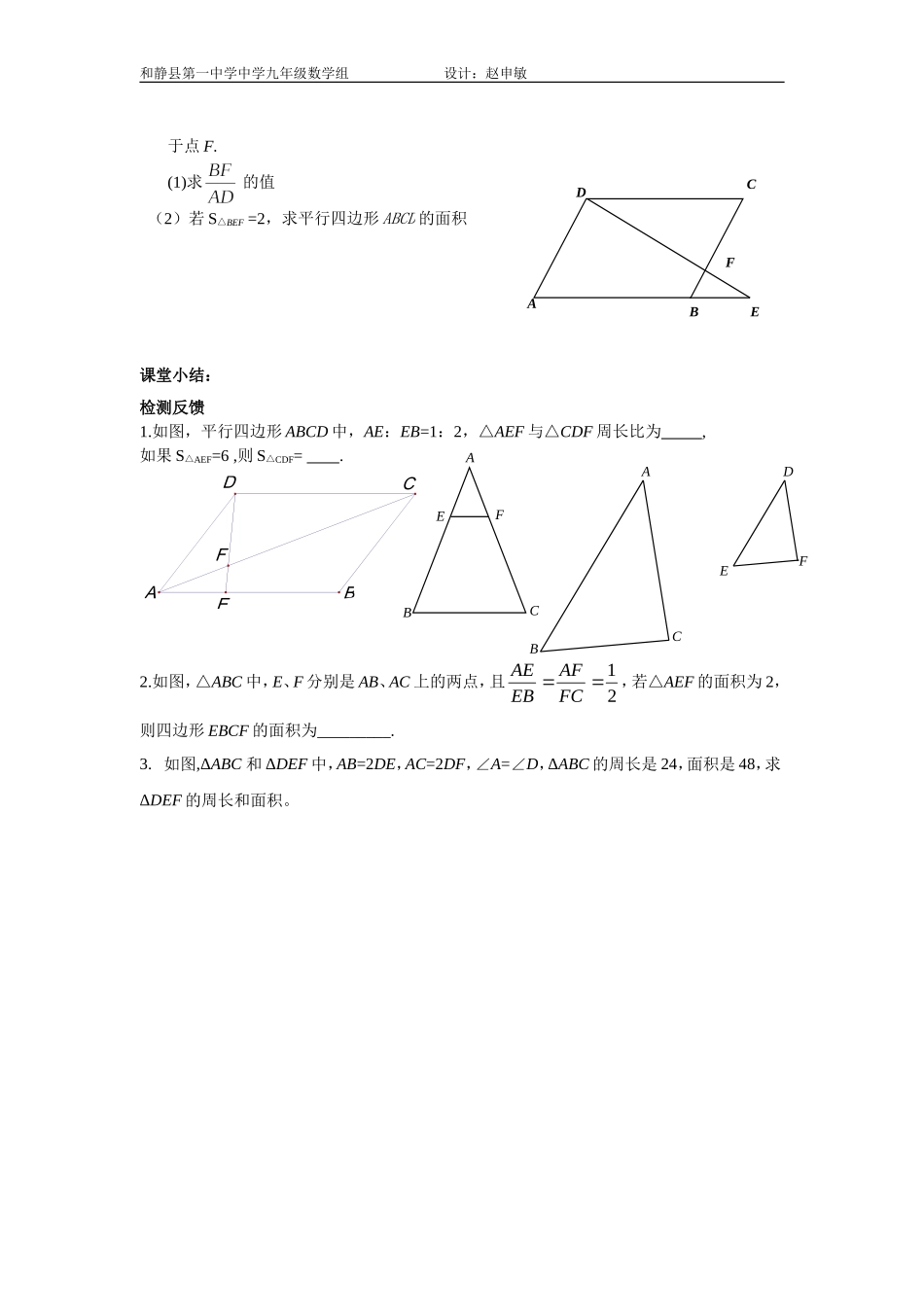
C'A'ACBB'和静县第一中学中学九年级数学组设计:赵申敏课题:27.2.2相似三角形的性质学习目标:1.了解相似三角形对应线段的比等于相似比;2.了解相似三角形面积比等于相似比的平方;3.会用相似三角形的性质解决相关问题.活动方案:活动一:知道“相似三角形对应线段的比等于相似比,面积比等于相似比的平方”勇于探究,挑战自我1.如图:ΔABC∽ΔA′B′C′,相似比为k,猜测一下它们的对应高、对应中线、对应角平分线的比以及周长比和面积比分别是多少.选一个你喜欢的结论说明理由,小组内交流.通过探究你得到的结论是:1.相似三角形对应线段的比等于.2.相似三角形周长的比等于.3.相似三角形面积的比等于.2.练习(1)已知ΔABC与ΔDEF的相似比为2:3,则对应中线的比为,对应角平分线的比为,周长比为,面积比为.(2)已知ΔABC∽ΔA′B′C′,面积比为16:9,则相似比为,对应高的比为,周长比为。(3)已知ΔABC∽ΔA′B′C′它们对应中线的比为1:3,ΔABC的面积为2,周长为4,则ΔA′B′C′的面积等于,周长等于.活动二:运用新知,提升自我1.如图,在ΔABC和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D.若ΔABC的边BC上的中线为8,面积为40,求ΔDEF的边EF上的中线和面积.2.如图,点E是平行四边形ABCD的边AB的延长线上一点,且AB=4BE,连接DE交BCAA'C'D'B'CDBAA'C'D'B'CDBAA'C'D'B'CDBEFDCBAFBCDAE和静县第一中学中学九年级数学组设计:赵申敏于点F.(1)求的值(2)若S△BEF=2,求平行四边形ABCD的面积课堂小结:检测反馈1.如图,平行四边形ABCD中,AE:EB=1:2,△AEF与△CDF周长比为,如果S△AEF=6,则S△CDF=.2.如图,△ABC中,E、F分别是AB、AC上的两点,且21FCAFEBAE,若△AEF的面积为2,则四边形EBCF的面积为_________.3.如图,ΔABC和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是48,求ΔDEF的周长和面积。ACBEDFAEFBCEFDCBA