弧、弦、圆心角VIP免费

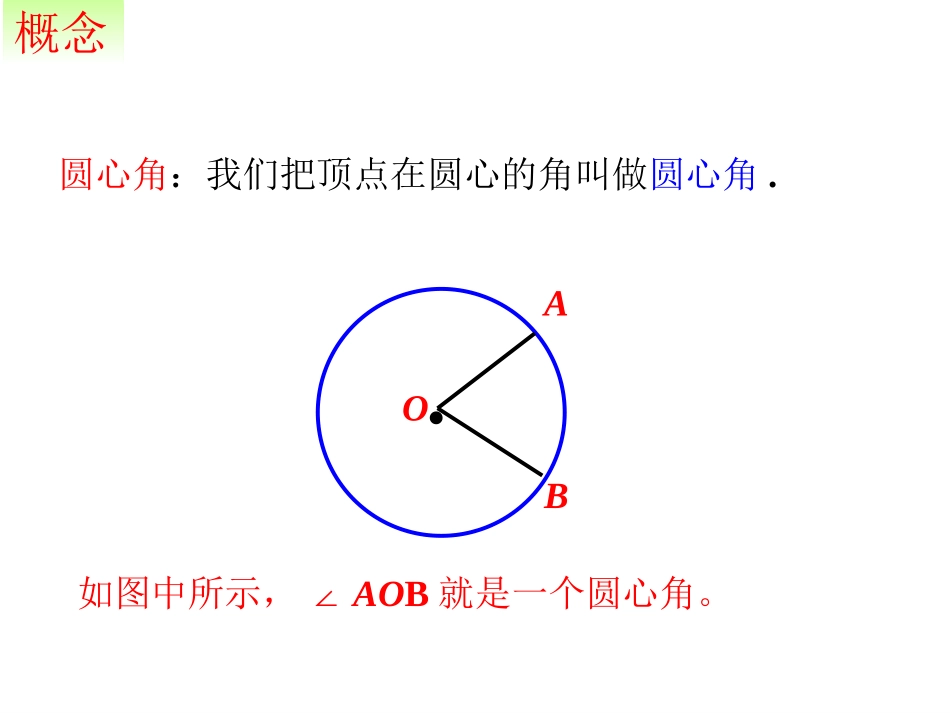
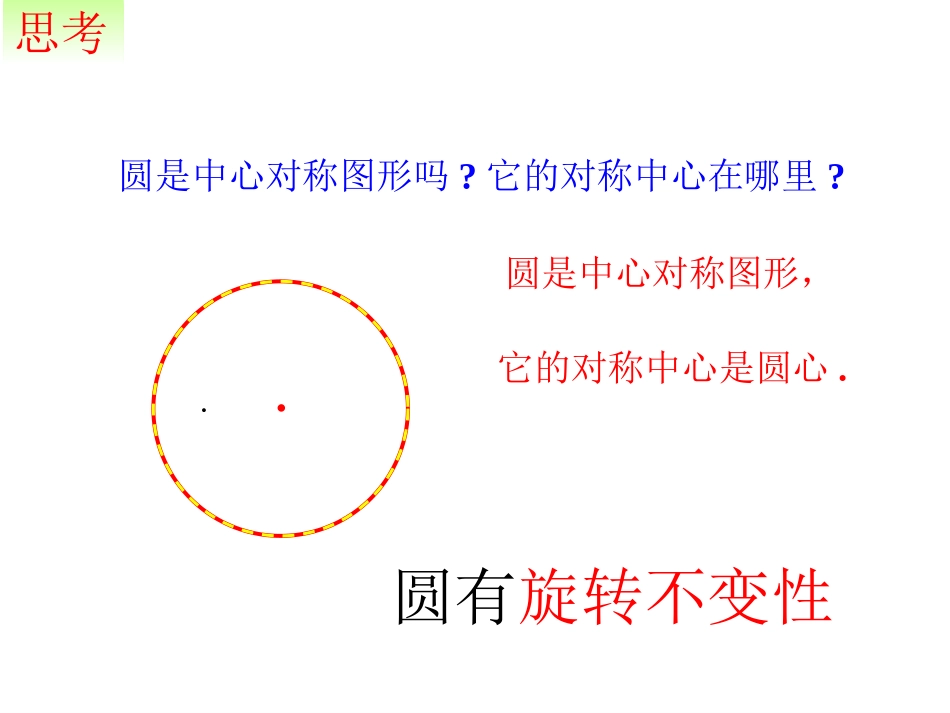
·圆心角：我们把顶点在圆心的角叫做圆心角.OBA概念如图中所示，∠AOB就是一个圆心角。圆是中心对称图形吗?它的对称中心在哪里?·思考圆是中心对称图形，它的对称中心是圆心.圆有旋转不变性根据旋转的性质，将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时，∠AOB＝∠A′OB′，射线OA与OA′重合，OB与OB′重合．而同圆的半径相等，OA=OA′，OB=OB′，∴点A与A′重合，B与B′重合．·OAB·OABA′B′A′B′∴重合，AB与A′B′重合．''ABAB与如图，将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置，你能发现哪些等量关系？为什么？探究'',ABAB''.ABAB∴在同圆或等圆中，相等的弧所对的圆心角____，所对的弦____；在同圆或等圆中，相等的弦所对的圆心角____，所对的弧____．弧、弦与圆心角的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．相等相等相等相等前提条件定理同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量也相等。同圆或等圆中圆心角等弧等弦等圆心角等弧等弦等圆心角等弧等弦等1.如图，AB、CD是⊙O的两条弦．（1）如果AB=CD，那么_________，____________．（2）如果，那么________，____________．（3）如果∠AOB=COD∠，那么________，________．（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？·CABDEFOAOBCODAB=CDAOBCODAB=CD练习AB=CD︵︵AB=CD︵︵AB=CD︵︵OE＝OF2.判断下列说法是否正确：①相等的圆心角所对的弧相等。（）②相等的弧所对的弦相等。（）③相等的弦所对的弧相等。（）3.如图，⊙O中，AB=CD，∠1＝50°，则∠2＝。×50°×√︵︵练习4.如图，AB是⊙O的直径，，∠COD=35°，求∠AOE的度数．·AOBCDE35BOCCODDOE180335AOE75解：BC=CD=DE︵︵︵练习∵BC=CD=DE︵︵︵1°弧n°1°n°弧把圆心角等分成360份,则每一份的圆心角是1°，同时整个圆也被分成了360份。则每一份这样的弧叫做1°的弧。这样，1º的圆心角对着1º的弧，1º的弧对着1º的圆心角。nº的圆心角对着nº的弧，nº的弧对着nº的圆心角。圆心角度数定理：圆心角的度数和它所对弧的度数相等.概念1°的弧：不同圆中，相同的圆心角所对的弧度数相同。例如半圆度数都是180。（2）AB所对的圆心角和CD所对的圆心角相等（）在两个圆中，分别有AB和CD，若AB的度数和CD的度数相等，则有（1）AB和CD相等（）练习1.判断正误︵︵︵︵︵︵︵︵(第1题)2.如图，在⊙O中，AB＝AC，∠B＝70°，求∠C的度数.练习︵︵3.如图，已知在⊙O中，OA⊥OB，∠A=35°，求BC与CD的度数。练习︵︵123∠1＝55°∠2＝70°BC的度数＝70°︵∠3＝20°CD的度数＝20°︵变式：如图，已知AD=BC，求证：AB=CD。例1如图，如果AD=BC，求证：AB＝CD。︵︵例题例2已知AB，CD是⊙O的两条直径，过点A作AE//CD，交⊙O于E，连接DB，DE。求证：DB=DE。例题123例3如图，在⊙O中，AB=AC，∠ACB=60°，求证：∠AOB=∠BOC=∠AOC.证明：∴AB＝AC又∠ACB=60°，∴△ABC是等边三角形∴AB＝BC＝AC·ABCO例题︵︵∵AB＝AC︵︵∴∠AOB＝∠BOC＝∠AOC.例4如图，在⊙O中，弦AB所对的劣弧为圆的，圆的半径为4，求AB的长例题E4313例例55已知已知ABAB是⊙是⊙OO的直径，的直径，MM、、NN分别是分别是AAOO和和BOBO的中点，的中点，CMCM⊥⊥ABAB，，DNDN⊥⊥ABAB，则，则ACAC和和BDBD有什么关系？为什么？有什么关系？为什么？︵︵例题AC＝BD︵︵例例66如图，如图，CDCD是是⊙⊙OO的弦，的弦，ACAC==BDBD，，OAOA、、OBOB分别交分别交CDCD于于EE、、FF，，求证：求证：OEOE＝＝OFOF。。⌒⌒⌒⌒例题拓展：拓展：如图所示，如图所示，CDCD为⊙为⊙OO的弦，在的弦，在CDCD上上取取CECE==DFDF，连结，连结OEOE、、OFOF，并延长交，并延长交⊙⊙OO于点于点AA、、BB。。（（11）试判断△）试判断△OEFOEF的的形状，并说明理由；形状，并说明理由；（（22）求证：）求证：ACAC==BDBD⌒⌒⌒⌒例题1.如图，已知AB、CD是⊙O中互相垂直的两条直径，又两条弦AE⊥CF于点G，求证：AE=CF。思考题G2.如图，已知⊙O中，AB=2CD，试判断AB与2CD的大小关系，并证明你的结论。思考题AB＜2CD⌒⌒⌒⌒M·3.如图，⊙O中AB是直径，COAB，D是CO的中点，DE//AB，求证：EC=2AE。⌒⌒⌒⌒思考题4.如图，点O是∠MPN的平分线上一点，以O为圆心的圆和PM、PN分别交于A、B、C、D，求证∠OBA＝∠OCD。EF12△BOE≌△COF（HL）思考题