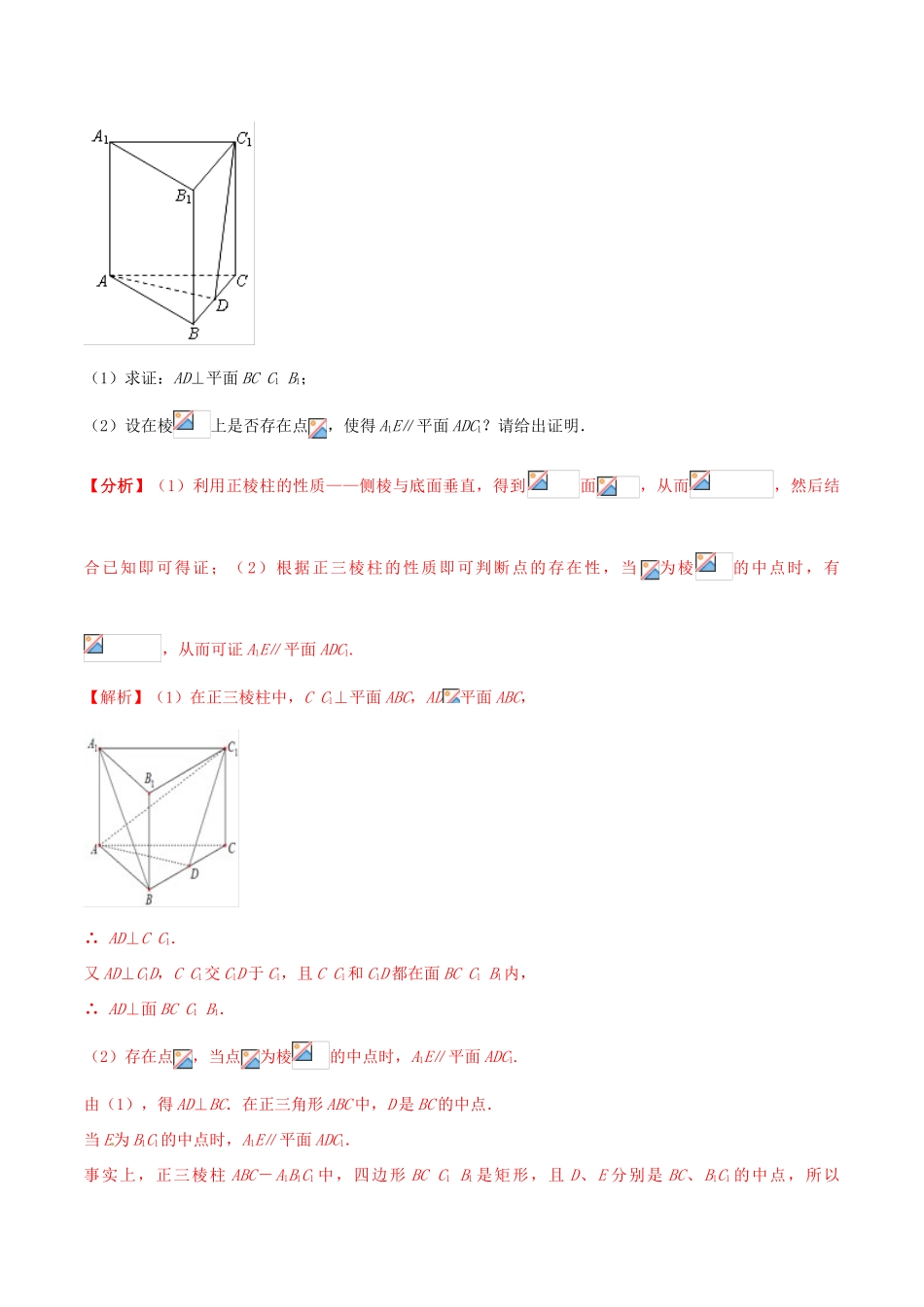
问题30转化与化归思想解决立体几何中的探索性问题一、考情分析立体几何中的探究性问题既能够考查学生的空间想象力,又可以考查学生的意志力和探究意识,逐步成为近几年高考命题的热点和今后命题的趋势之一,探究性问题主要有两类:一是推理型,即探究空间中的平行与垂直关系,可以利用空间线面关系的判定与性质定理进行推理探究;二是计算型,即对几何体中的空间角与距离、几何体的体积等计算型问题的有关探究,此类问题多通过求角、求距离、体积等的基本方法把这些探究性问题转化为关于某个参数的方程,根据方程解的存在性来解决.二、经验分享1.对命题条件的探索常采用以下三种方法:(1)先猜后证,即先观察与尝试给出条件再给出证明.(2)先通过命题成立的必要条件探索出命题成立的条件,再证明充分性.(2)把几何问题转化为代数问题,探索出命题成立的条件.2.对于存在判断型问题,解题的策略一般为先假设存在,然后转化为“封闭型”问题求解判断,若不出现矛盾,则肯定存在;若出现矛盾,则否定存在.这是一种最常用也是最基本的方法对命题结论的探索,常从条件出发,探索出要求的结论是什么,另外还有探索的结论是否存在.求解时,常假设结论存在,再寻找与条件相容还是矛盾的结论.3.解决立体几何中的探索性问题的步骤:第一步:写出探求的最后结论;第二步:证明探求结论的正确性;第三步:给出明确答案;第四步:反思回顾,查看关键点、易错点和答题规范.三、题型分析(一)空间线面关系的探索性问题1.空间平行关系的探索性问题【例1】如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.(1)求证:AD⊥平面BCC1B1;(2)设在棱上是否存在点,使得A1E∥平面ADC1?请给出证明.【分析】(1)利用正棱柱的性质——侧棱与底面垂直,得到面,从而,然后结合已知即可得证;(2)根据正三棱柱的性质即可判断点的存在性,当为棱的中点时,有,从而可证A1E∥平面ADC1.【解析】(1)在正三棱柱中,CC1⊥平面ABC,AD平面ABC,∴AD⊥CC1.又AD⊥C1D,CC1交C1D于C1,且CC1和C1D都在面BCC1B1内,∴AD⊥面BCC1B1.(2)存在点,当点为棱的中点时,A1E∥平面ADC1.由(1),得AD⊥BC.在正三角形ABC中,D是BC的中点.当E为B1C1的中点时,A1E∥平面ADC1.事实上,正三棱柱ABC-A1B1C1中,四边形BCC1B1是矩形,且D、E分别是BC、B1C1的中点,所以B1B∥DE,B1B=DE.又B1B∥AA1,且B1B=AA1,∴DE∥AA1,且DE=AA1.所以四边形ADEA1为平行四边形,所以EA1∥AD.而EA1面ADC1内,故A1E∥平面ADC1.【点评】线面平行与垂直是高考考查空间线面关系证明的两个重点,此类探究性问题的求解,一定要灵活利用空间几何体的结构特征,注意其中的平行与垂直关系,如该题中正棱柱中侧棱与底面垂直关系的应用;为棱的中点时,有等的灵活应用,帮助我们能够准确地判断探究性问题的结论,丙直接迅速地把握证明的思路.【小试牛刀】【湖南省怀化市2019届高三3月第一次模拟】如图,四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,为侧棱上的点.(1)求证:;(2)若平面,求二面角的大小;(3)在(2)的条件下,侧棱上是否存在一点,使得平面.若存在,求的值;若不存在,试说明理由.【解析】(1)连交于,由题意.在正方形中,,所以平面,得(2)由题设知,连,设交于于,由题意知平面.以为坐标原点,,,分别为轴、轴、轴正方向,建立坐标系如图.设底面边长为,则高.则,,又平面,则平面的一个法向量,平面的一个法向量,则,又二面角为锐角,则二面角为;(3)在棱上存在一点使平面.由(2)知是平面的一个法向量,且,设,则又平面,所以,则.即当时,而不在平面内,故平面.2.空间垂直关系的探索性问题【例2】棱长为2的正方体中,E为棱的中点,F为棱的中点.(1)求证:;(2)求在线段上是否存在点G,使⊥面DFG.?试证明你的结论.【分析】(1)先根据正方体的性质得到,,进而证明面,故可得到结论;(2)首先根据正方体的结构特征确定点G的存在性和具体位置,然后进行证明.【解析】(1)连接,,由正方体的性质可知,,所以面,所以.(2)存在点G,当点G为点,⊥面DFG.证明如下:由(1)知,取CD的中点H,连AH,EH.由DFA...