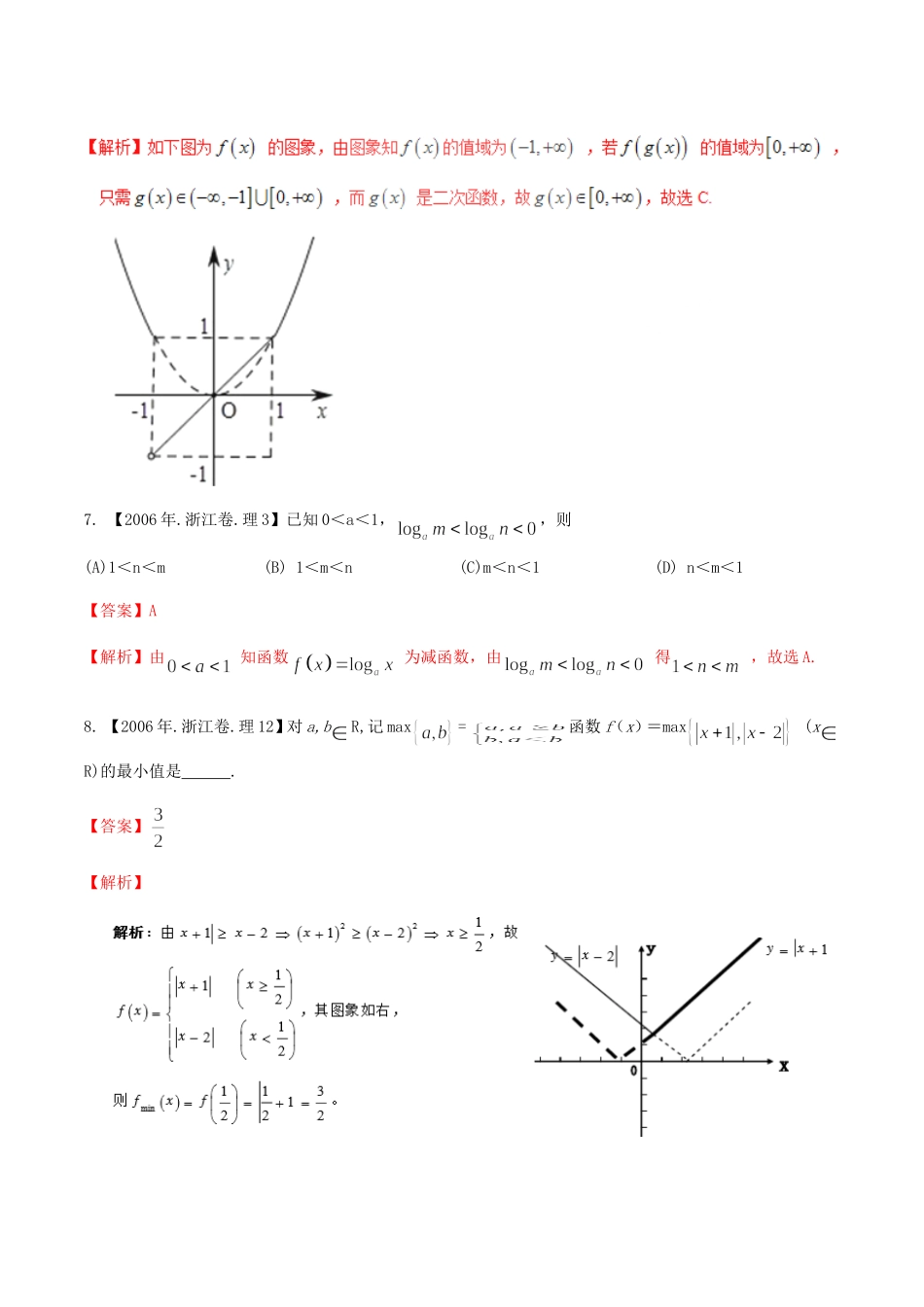
第二章函数一.基础题组1.【2014年.浙江卷.理6】已知函数()A.B.C.D.【答案】:C2.【2013年.浙江卷.理3】已知x,y为正实数,则().A.2lgx+lgy=2lgx+2lgyB.2lg(x+y)=2lgx·2lgyC.2lgx·lgy=2lgx+2lgyD.2lg(xy)=2lgx·2lgy【答案】:D【解析】:根据指数与对数的运算法则可知,2lgx+lgy=2lgx·2lgy,故A错,B错,C错;D中,2lg(xy)=2lgx+lgy=2lgx·2lgy,故选D.3.【2012年.浙江卷.理9】设a>0,b>0,()A.若2a+2a=2b+3b,则a>bB.若2a+2a=2b+3b,则a<bC.若2a-2a=2b-3b,则a>bD.若2a-2a=2b-3b,则a<b【答案】A【解析】考查函数y=2x+2x为单调递增函数,若2a+2a=2b+2b,则a=b,若2a+2a=2b+3b,则a>b.4.【2011年.浙江卷.理1】设函数,则实数=(A)-4或-2(B)-4或2(C)-2或4(D)-2或2【答案】B【解析】:当,故选B5.【2011年.浙江卷.理11】若函数为偶函数,则实数。【答案】06.【2007年.浙江卷.理10】设,是二次函数,若的值域是,则的值域是(A)(B)(C)(D)【答案】C7.【2006年.浙江卷.理3】已知0<a<1,,则(A)1<n<m(B)1<m<n(C)m<n<1(D)n<m<1【答案】A【解析】由知函数为减函数,由得,故选A.8.【2006年.浙江卷.理12】对a,bR,记max=函数f(x)=max(xR)的最小值是.【答案】【解析】9.【2005年.浙江卷.理3】设f(x)=,则f[f()]=()(A)(B)(C)-(D)【答案】B【解析】:f[f()]=f[|-1|-2]=f[-]=,选(B)二.能力题组1.【2014年.浙江卷.理7】在同意直角坐标系中,函数的图像可能是()【答案】:D考点:函数图像.2.【2014年.浙江卷.理15】设函数若,则实数的取值范围是______【答案】:3.【2011年.浙江卷.理10】设,,为实数,=,=.记集合S=,=,若,分别为集合元素S,T的元素个数,则下列结论不可能的是(A)=1且=0(B)(C)=2且=2(D)=2且=3【命题意图】本题结合集合知识考查函数零点的概念,难度较大.4.【2010年.浙江卷.理10】设函数的集合,平面上点的集合,则在同一直角坐标系中,中函数的图象恰好经过中两个点的函数的个数是(A)4(B)6(C)8(D)10【答案】B5.【2009年.浙江卷.理14】某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:高峰时间段用电价格表低谷时间段用电价格表高峰月用电量(单位:千瓦时)高峰电价(单位:元/千瓦时)低谷月用电量(单位:千瓦时)低谷电价(单位:元/千瓦时)50及以下的部分0.56850及以下的部分0.288超过50至200的部分0.598超过50至200的部分0.318超过200的部分0.668超过200的部分0.388若某家庭5月份的高峰时间段用电量为千瓦时,低谷时间段用电量为千瓦时,则按这种计费方式该家庭本月应付的电费为元(用数字作答).【答案】:6.【2008年.浙江卷.理15】已知t为常数,函数在区间[0,3]上的最大值为2,则t=。【答案】1.7.【2006年.浙江卷.理10】函数满足f(f(x))=f(x),则这样的函数个数共有(A)1个(B)4个(C)8个(D)10个【答案】D8.【2006年.浙江卷.理16】设f(x)=3ax,f(0)>0,f(1)>0,求证:(Ⅰ)a>0且-2<<-1;(Ⅱ)方程f(x)=0在(0,1)内有两个实根.【答案】详见解析.9.【2005年.浙江卷.理16】已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.(Ⅰ)求函数g(x)的解析式;(Ⅱ)解不等式g(x)≥f(x)-|x-1|.【答案】(Ⅰ)g(x)=-x2+2x;(Ⅱ)不等式的解集为[-1,]10.【2015高考浙江,理7】存在函数满足,对任意都有()A.B.C.D.【答案】D.11.【2015高考浙江,理18】已知函数,记是在区间上的最大值.(1)证明:当时,;(2)当,满足,求的最大值.【答案】(1)详见解析;(2).,由,得,当,时,,且在上的最大值为,即,∴的最大值为..【考点定位】1.二次函数的性质;2.分类讨论的数学思想.12.三.拔高题组1.【2014年.浙江卷.理10】设函数,,,记,则()A.B.C.D.答案:B2.【2015高考浙江,理12】若,则.【答案】.【解析】∵,∴,∴.【考点定位】对数的计算3.【2015高考浙江,理10】已知函数,则,的最小值是.【答案】,.4.