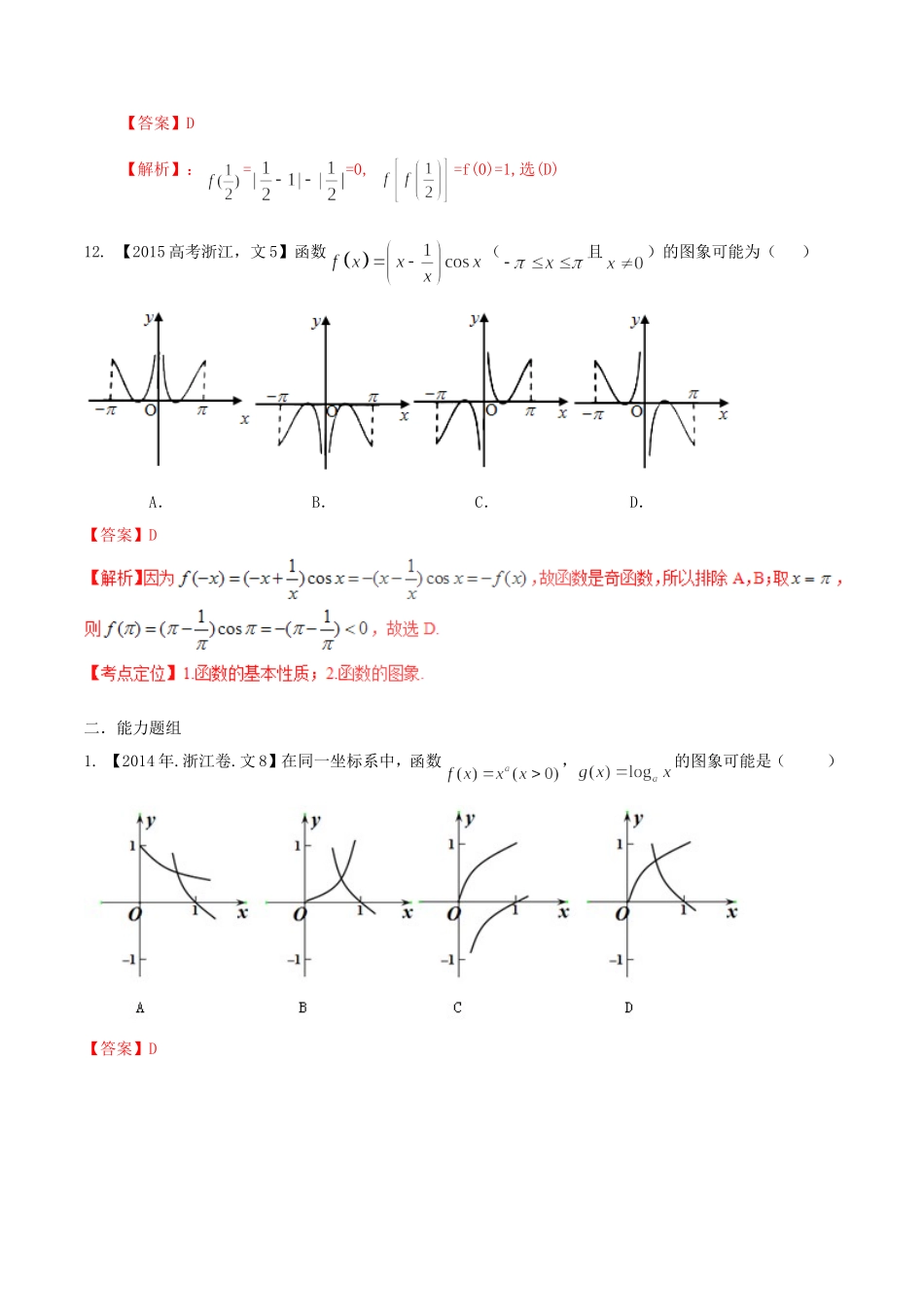
第二章函数一.基础题组1.【2014年.浙江卷.文7】已知函数,且,则()A.B.C.D.【答案】C2.【2014年.浙江卷.文15】设函数,若,则.【答案】3.【2013年.浙江卷.文7】已知a,b,c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)>f(1),则().A.a>0,4a+b=0B.a<0,4a+b=0C.a>0,2a+b=0D.a<0,2a+b=0【答案】:A4.【2013年.浙江卷.文11】已知函数f(x)=.若f(a)=3,则实数a=__________.【答案】:10【解析】:由f(a)==3,得a-1=9,故a=10.5.【2012年.浙江卷.文16】设函数f(x)是定义在R上的周期为2的偶函数,当x∈[0,1]时,f(x)=x+1,则__________.【答案】【解析】6.【2011年.浙江卷.文11】设函数,若,则实数=____【答案】【解析】:7.【2010年.浙江卷.文2】已知函数若=(A)0(B)1(C)2(D)3【答案】B8.【2008年.浙江卷.文11】已知函数2()|2|fxxx,则(1)f__________.【答案】2【解析】:本小题主要考查知函数解析式,求函数值问题.代入求解即可.9.【2007年.浙江卷.文11】函数的值域是______________.【答案】:10.【2006年.浙江卷.文4】已知,则(A)n<m<1(B)m<n<1(C)1<m<n(D)1<n<m【答案】D11.【2005年.浙江卷.文4】设,则=()(A)(B)0(C)(D)1【答案】D【解析】:==0,=f(0)=1,选(D)12.【2015高考浙江,文5】函数(且)的图象可能为()A.B.C.D.【答案】D二.能力题组1.【2014年.浙江卷.文8】在同一坐标系中,函数,的图象可能是()【答案】D2.【2012年.浙江卷.文10】设a>0,b>0,e是自然对数的底数()A.若ea+2a=eb+3b,则a>bB.若ea+2a=eb+3b,则a<bC.若ea-2a=eb-3b,则a>bD.若ea-2a=eb-3b,则a<b【答案】A3.【2010年.浙江卷.文9】已知是函数=的一个零点.若∈(1,),∈(,+),则(A)<0,<0(B)<0,>0(C)>0,<0(D)>0,>0【答案】B【解析】:作出=和=的图像,由图像知,当∈(1,),∈(,+)时,<0,>0,故选B.考察了数形结合的思想,以及函数零点的概念和零点的判断,属中档题4.【2009年.浙江卷.文8】若函数,则下列结论正确的是()A.,在上是增函数B.,在上是减函数C.,是偶函数D.,是奇函数【答案】C【解析】对于时有是一个偶函数5.【2009年.浙江卷.文15】某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:高峰时间段用电价格表低谷时间段用电价格表高峰月用电量(单位:千瓦时)高峰电价(单位:元/千瓦时)低谷月用电量(单位:千瓦时)低谷电价(单位:元/千瓦时)50及以下的部分0.56850及以下的部分0.288超过50至200的部分0.598超过50至200的部分0.318超过200的部分0.668超过200的部分0.388若某家庭5月份的高峰时间段用电量为千瓦时,低谷时间段用电量为千瓦时,则按这种计费方式该家庭本月应付的电费为元(用数字作答).【答案】6.【2006年.浙江卷.文10】对a,bR,记max{a,b}=,函数f(x)=max{|x+1|,|x-2|}(xR)的最小值是(A)0(B)(C(D)3【答案】C7.【2015高考浙江,文9】计算:,.【答案】三.拔高题组1.【2007年.浙江卷.文22】(本题15分)已知.(I)若k=2,求方程的解;(II)若关于x的方程在(0,2)上有两个解x1,x2,求k的取值范围,并证明【答案】(Ⅰ)解:(1)当k=2时,①当时,即≥1或≤-1时,方程化为解得,因为,故舍去,所以.②当时,-1<<1时,方程化为解得2.【2006年.浙江卷.文20】设,,f(0)f(1)>0,求证:(Ⅰ)方程有实根。(Ⅱ)-2<<-1;(III)设是方程f(x)=0的两个实根,则.【答案】详见解析.【解析】证明:(Ⅰ)若a=0,则b=-c,f(0)f(1)=c(3a+2b+c),与已知矛盾,所以a≠0.3.【2005年.浙江卷.文20】已知函数和的图象关于原点对称,且.(Ⅰ)求函数的解析式;(Ⅱ)解不等式;(Ⅲ)若在上是增函数,求实数的取值范围.【答案】(Ⅰ)g(x)=-x2+2x;(Ⅱ)不等式的解集为[-1,];(Ⅲ)λ≤0.【解析】:(Ⅰ)设函数y=f(x)的图象上任一点Q(xqλ,yq关于原点的对称点(x,y),则即∵点Qxq,yq)在函数f(x)的图象上,∴-y=-x2+2x.,故g(x)=-x2+2x(Ⅱ)由g(x)≥f(x)-|x-1|可得2x2-|x-1|≤0,当x≥1时,2x2-x+1≤0,此时不等式无解,当x<1时,2x2+x-1≤0,∴-1≤x≤,因此,原不等式的解集为[-1,](Ⅲ)h(x)=-(1+λ)x2+2(1-λ)x+1①当λ=-1时,h(x)=4x+1在[-1,1]上是增函数,∴λ=-1②当λ≠-1时,对称轴的方程为x=.(i)当λ<-1时,≤-1,解得λ<-1.(ii)当λ>-1时,≥-1,解得-1<λ≤0.综上,λ≤04.【2015高考浙江,文12】已知函数,则,的最小值是.【答案】