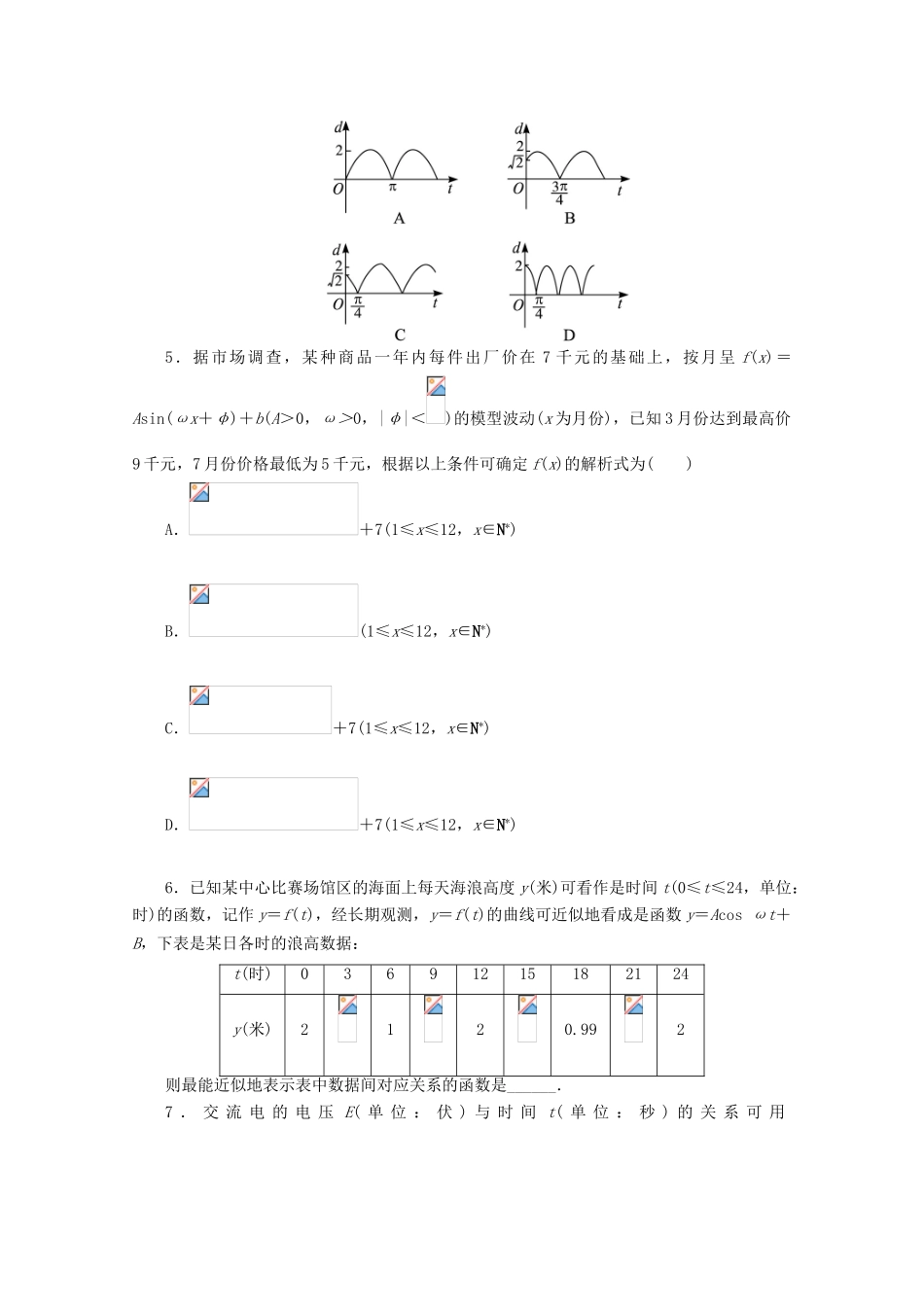
高中数学3.4.3应用举例同步练习湘教版必修21.电流I(A)随时间t(s)变化的关系式是,则当s时,电流I等于()A.5AB.2.5AC.2AD.-5A2.弹簧上挂的小球做上下振动,它在时间t(秒)时离开平衡位置的距离s(厘米)满足函数关系式,有如下三种说法:①小球开始在平衡位置上方厘米处;②小球下降到最低点时在平衡位置下方2厘米处;③经过2π秒小球重复振动一次.其中正确的说法是()A.①②B.②③C.①③D.①②③3.下表是某城市月平均气温(华氏度):月份123456平均气温21.426.036.048.859.168.6月份789101112平均气温73.171.964.753.539.827.7若用x表示月份,y表示平均气温,则下面四个函数模型中最合适的是()A.B.+46C.+46D.+264.如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(,),角速度为1rad/s,那么点P到x轴的距离d关于时间t的函数图象大致为()5.据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈f(x)=Asin(ωx+φ)+b(A>0,ω>0,|φ|<)的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定f(x)的解析式为()A.+7(1≤x≤12,x∈N*)B.(1≤x≤12,x∈N*)C.+7(1≤x≤12,x∈N*)D.+7(1≤x≤12,x∈N*)6.已知某中心比赛场馆区的海面上每天海浪高度y(米)可看作是时间t(0≤t≤24,单位:时)的函数,记作y=f(t),经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+B,下表是某日各时的浪高数据:t(时)03691215182124y(米)2120.992则最能近似地表示表中数据间对应关系的函数是______.7.交流电的电压E(单位:伏)与时间t(单位:秒)的关系可用来表示.则电压值的最大值是________,第一次获得这个最大值的时间是________.8.如图,是一弹簧振子做简谐运动的图象,其解析式为y=Asin(ωx+φ)(A>0,ω>0,|φ|<),横轴表示振动的时间,纵轴表示振子的位移,则这个振子振动的函数解析式是__________.9.心脏跳动时,血压在增加或减小,血压的最大值,最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数120/80mmHg高为标准值,设某人的血压近似满足P(t)=115+25sin160πt,其中P(t)为血压(mmHg高),t为时间(min),试回答问题:(1)求函数P(t)的周期;(2)此人每分钟心跳的次数;(3)利用函数式求出此人的血压,并与标准值比较.参考答案1.答案:B解析:当s时,==2.5(A).2.答案:D解析:当t=0时,,①正确;smin=-2,②正确;T=2π,③正确.3.答案:C解析:通过表可以看到周期T=12,,分别代入检验,可知C模型最合适.4.答案:C解析:P从P0出发,逆时针运动,t=0时,,t与d满足关系式(t≥0).所以选择C.5.答案:A解析:令x=3可排除D,令x=7可排除B,由A==2可排除C;或由题意,可得A==2,b=7,周期T==2×(7-3)=8,∴.∴+7.∵当x=3时,y=9,∴+7=9,即.∵,∴.∴+7(1≤x≤12,x∈N*).6.答案:解析:设函数的关系式为y=Acosωt+B.∵周期为T=12,∴,,.∴.7.答案:伏秒解析:电压值的最大值为伏.由得,所以第一次获得最大值的时间是秒.8.答案:解析:A=2,T=2×(0.5-0.1)=0.8,∴.又×0.1+φ=,∴.∴解析式为.9.解:∵P(t)=115+25sin160πt,∴(1).(2)此人每分钟心跳次数为f==80(次).(3)当sin160πt=1时,收缩压为115+25=140(mmHg高).当sin160πt=-1时,舒张压为115-25=90(mmHg高).又∵收缩压和舒张压的标准值为120/80mmHg高,∴此人的收缩压和舒张压均高于相应的标准值.