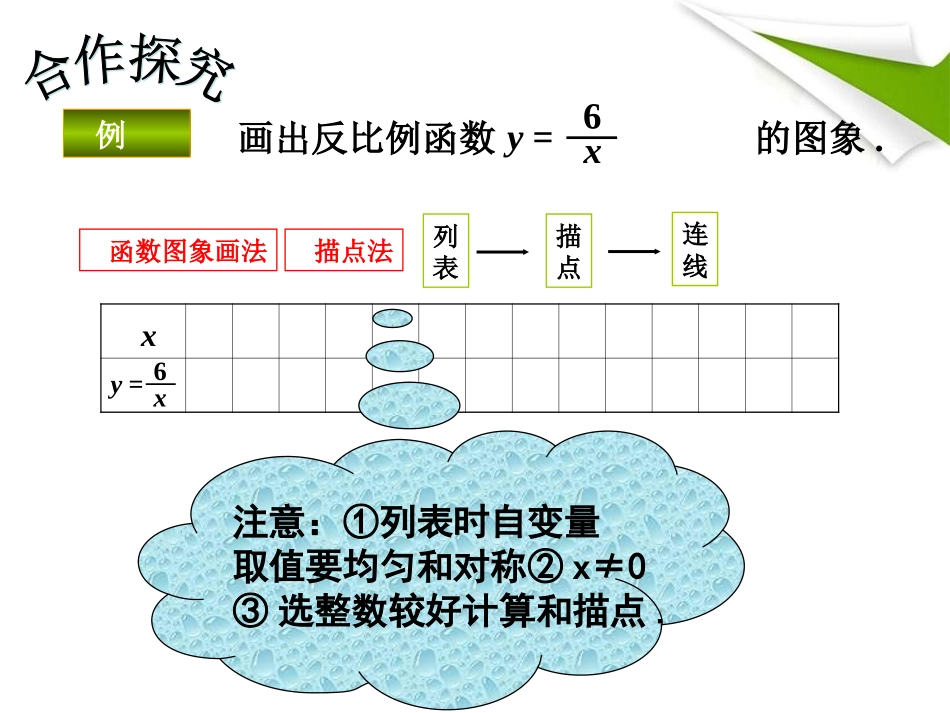
1.2反比例函数的图象与性质第1课时反比例函数的图象与性质(0)kykx“预见性”,猜一猜反比例函数的图象又会是什么样子呢?你还记得作函数图象的一般步骤吗?给反比例函数“照相”回顾与思考,,,0.xykykkyxx一般地如果两个变量之间的关系可以表示成为常数的形式,那么称是的反比例函数用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).xy=x6注意:①列表时自变量取值要均匀和对称②x≠0③选整数较好计算和描点.函数图象画法列表描点连线描点法画出反比例函数的图象.y=x6例xy=x6123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.261-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………y=x6观察图形,y轴右边的点,当横坐标x逐渐增大时,纵坐标y如何变化?y轴左边的各点是否也有相同的规律?结论对于反比例函数,当x>0时,函数值y随自变量x的增大而减小;当x<0时,也有这一规律.y=x6你认为作反比例函数图象时应注意哪些问题?•列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;•列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;•连线时,一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性;•……说一说在下面的直角坐标系内,画出反比例函数的图象.y=x3123456-1-3-2-4-5-61234-1-2-3-40-6-556xyx…………解列表:2153432323435321描点、画图:3y=x3y=x1-331123456-1-2-3-4-5-6动脑筋(1)每个函数的图象分别位于哪些象限?(2)在每一象限内,函数值y随自变量x的变化如何变化?观察画出的,的图象,思考下列问题:y=x3y=x6结论一般地,当k>0时,反比例函数的图象由分别在第一、三象限内的两支曲线组成,它们与x轴、y轴都不相交,在每个象限内,函数值y随自变量x的增大而减小.y=xk本节收获本节收获1.进一步巩固复习了作函数图象的一般方法和步骤;2.亲手画出函数的图象,用类比的方法,数形结合的思想,有了对图形进行观察、分析和归纳的体验,掌握了反比例函数的图象和性质;当k>0时,双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小.3.反比例函数(k为常数,k≠0)的图象是双曲线.xky已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是()o(A)(B)(C)(D)r/cmh/cmor/cmh/cmor/cmh/cmor/cmh/cm课后练习11C已知k>0,则函数y1=kx+k与y2=在同一坐标系中的图象大致是()xkC(A)xy0xy0(B)(C)(D)xy0xy0课后练习22