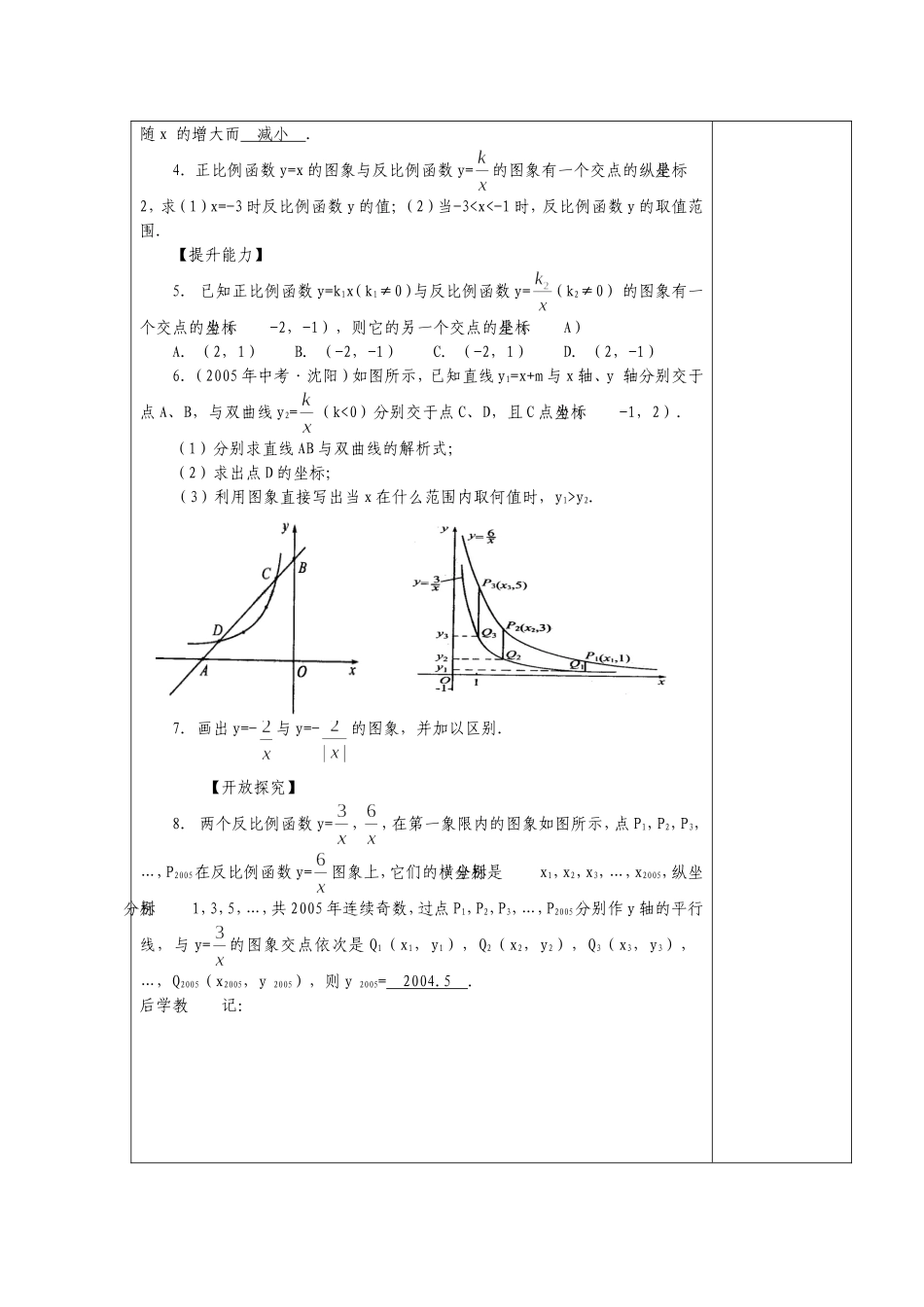
课题反比例函数的图象和性质(二)课型新授教学目标知识与技能巩固反比例函数图象的画法过程与方法继续结合图象分析并掌握反比例函数的性质,并用来解决相关的问题情感与态度体会函数的三种表示方法,进一步领会数形结合的思想方法,善于用数学知识解决身边的数学问题,提高学习数学的热情和积极性.教学重点理解、掌握、运用反比例函数的图象和性质教学难点反比例函数的图象和性质的灵活运用教具准备教学过程教师活动学生活动(一)创设情境、导入新课老师在黑板上写了这样一道题:“已知点(2,5)在反比例函数y=的图象上,试判断点(-5,-2)是否也在此图象上.”题中的“?”是被一个同学不小心擦掉的一个数字,请你分析一下“?”代表什么数,并解答此题目.(二)合作交流、解读探究探究点(2,5)在反比例函数图象上,其坐标当然满足函数解析式,因此,代入后易求得?=10,即反比例函数关系式为y=,再当x=-5时,代入易求得y=-2,说明点(-5,-2)适合此函数解析式,进而说明点(-5,-2)一定在其函数图象上.交流,与同学们分享成功的喜悦.(三)应用迁移、巩固提高例1已知反比例函数的图象经过点A(2,6)(1)这个函数的图象分布在哪些象限?y随x的增大而如何变化?(2)点B(3,4)、C(-2,-4)和D(2,5)是否在这个函数的图象上?解:(1)设这个反比例函数为y=,因为它过点A(2,6),所以把坐标代入得6=,解得k=12,此反比例函数式为y=,又因k=12>0,所以图象在第一、三象限,且在每个象限内,y随x的增大而减小.(2)把点B、C、D的坐标分别代入y=,知点B、C的坐标满足函数关系式,点D的坐标不满足函数关系式,所以点B、C在函数y=的图象上,点D不在这个函数的图象上.例2三个反比例函数(1)y=(2)y=(3)y=在x轴上方的图象如图所示,由此推出k1,k2,k3的大小关系例3直线y=kx与反比例函数y=-的图象相交于点A、B,过点A作AC垂直于y轴于点C,求S△ABC.解:反比例函数的图象关系原点对称,又y=kx过原点,故点A、B必关于原点对称,从而有OA=OB,所以S△AOC=S△BOC.设点A坐标为(x1,y1),则xy=-6,且由题意AC=│x1│,OC=│y1│.故S△AOC=AC·OC=│x1y1│=×6=3,从而S△ABC=2S△AOC=6.备选例题1.已知函数y=-kx(k≠0)和y=-的图象交于A、B两点,过点A作AC垂直于y轴,垂足为C,则S△BOC=.2.已知正比例函数y=kx和反比例函数y=的图象都过点A(m,1),求此正比例函数解析式及另一交点的坐标.(四)总结反思、拓展升华反比例函数的性质及运用(1)k的符号决定图象所在象限.(2)在每一象限内,y随x的变化情况,在不同象限,不能运用此性质.(3)从反比例函数y=的图象上任一点向一坐标轴作垂线,这一点和垂足及坐标原点所构成的三角形面积S△=│k│.(4)性质与图象在涉及点的坐标,确定解析式方面的运用.(五)课堂小练、跟踪反馈【夯实基础】1.判断下列说法是否正确(1)反比例函数图象的每个分支只能无限接近x轴和y轴,但永远也不可能到达x轴或y轴.(∨)(2)在y=中,由于3>0,所以y一定随x的增大而减小.(×)(3)已知点A(-3,a)、B(-2,b)、C(4,c)均在y=-的图象上,则ay2....