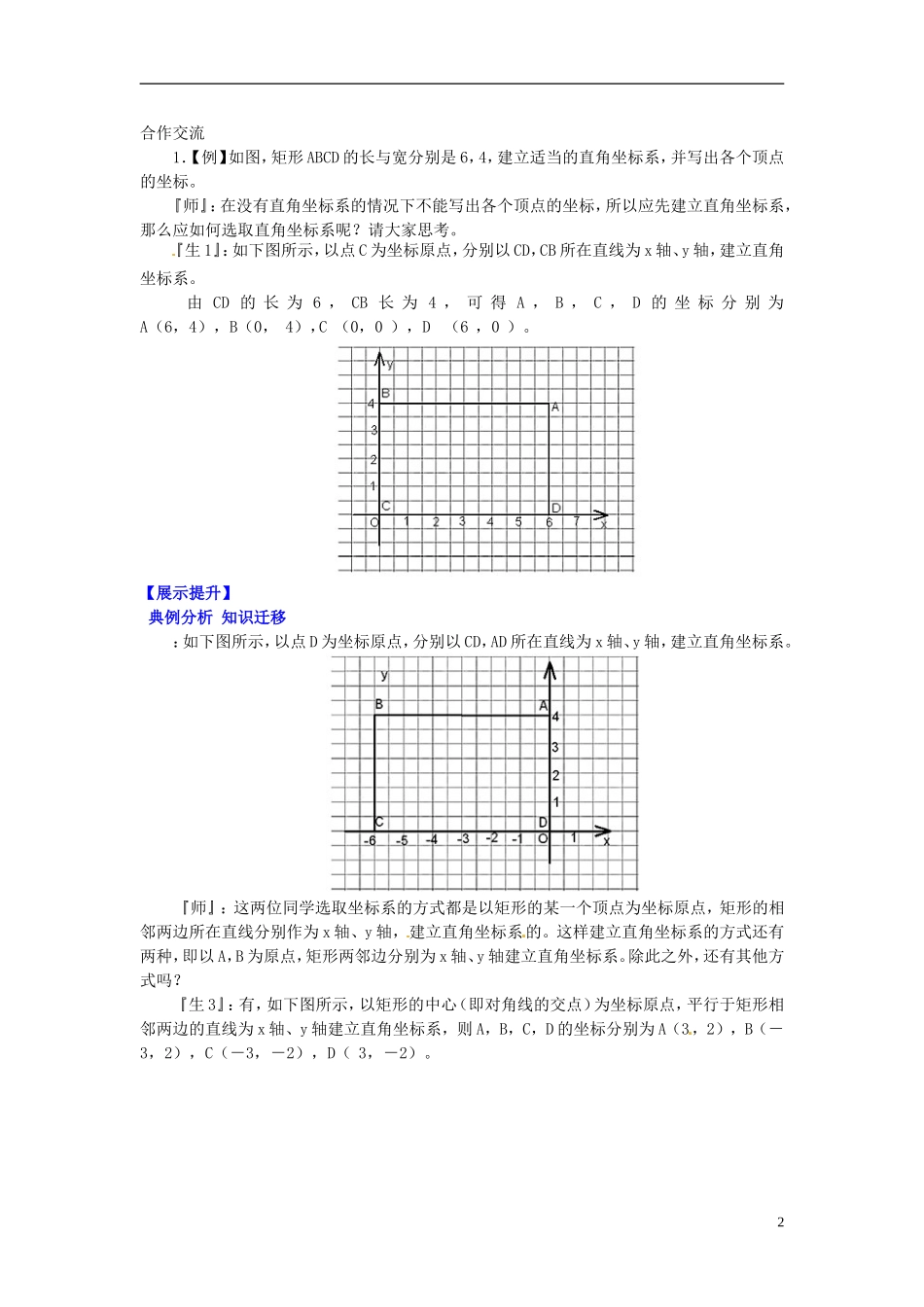
5.2平面直角坐标系(第3课时)【学习目标】课标要求:1.进一步巩固画平面直角坐标系,在给定的直角坐标系中,会根据坐标轴描出点的位置,由点的位置写出它的坐标。2.能在方格纸上建立适当的直角坐标系,描述物体的位置。3.能结合具体情景灵活运用多种方式确定物体的位置。目标达成:根据实际问题建立适当的坐标系,并能写出各点的坐标。探究式学习学习流程:【课前展示】必答题:1、在生活中,有哪些用哪些方法确定物体的位置?2、在平面内,确定一个物体的位置一般需要几个数据?3、在空间内,确定一个物体的位置一般需要几个数据?请举例说明.4.在平面内,下列数据不能确定物体位置的是()A.3楼5号B.北偏西40°C.解放路30号D.东经120°,北纬30°5.海事救灾船前去救援某海域失火轮船,需要确定()A.方位角B.距离C.失火轮船的国籍D.方位角和距离6、在已知坐标系中描出以下各点,并将各点用线段依次连接起来,观察A点与其他各点有什么特殊的位置关系:A(-1,2),B(1,2),C(-1,-2)D(1,-2)。抢答题:指出下列各点以及所在象限或坐标轴:A(-1,-2.5),B(3,-4),C(41,5),D(3,6),E(-2.3,0),F(0,32),G(0,0)(抽取学生作答)由点找坐标是已知点在直角坐标系中的位置,根据这点在方格纸上对应的x轴、y【创境激趣】内容:在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2)和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4,4),除此外不知道其他信息。如何确定直角坐标系找到宝藏?目的:这个情境具有一定趣味性和探究性,这样可以大大激发学生的思维,增强学生的学习兴趣,使学生进入快乐的学习中来,提高学生学习的积极性和主动性,同时引导学生进入新课的学习。教学处理:这里仅仅提出问题,激发兴趣,并不要求现在解决,而希望在本节课后面再回解该问题。【合作探究】自学导航】1合作交流1.【例】如图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标。『师』:在没有直角坐标系的情况下不能写出各个顶点的坐标,所以应先建立直角坐标系,那么应如何选取直角坐标系呢?请大家思考。『生1』:如下图所示,以点C为坐标原点,分别以CD,CB所在直线为x轴、y轴,建立直角坐标系。由CD的长为6,CB长为4,可得A,B,C,D的坐标分别为A(6,4),B(0,4),C(0,0),D(6,0)。【展示提升】典例分析知识迁移:如下图所示,以点D为坐标原点,分别以CD,AD所在直线为x轴、y轴,建立直角坐标系。『师』:这两位同学选取坐标系的方式都是以矩形的某一个顶点为坐标原点,矩形的相邻两边所在直线分别作为x轴、y轴,建立直角坐标系的。这样建立直角坐标系的方式还有两种,即以A,B为原点,矩形两邻边分别为x轴、y轴建立直角坐标系。除此之外,还有其他方式吗?『生3』:有,如下图所示,以矩形的中心(即对角线的交点)为坐标原点,平行于矩形相邻两边的直线为x轴、y轴建立直角坐标系,则A,B,C,D的坐标分别为A(3,2),B(-3,2),C(-3,-2),D(3,-2)。2『生4』:把上图中的横坐标逐渐向上、下移动,纵坐标左、右移动,则可得到不同的坐标系,从而得到A,B,C,D四点的不同坐标。『师』:从刚才我们讨论的情况看,大家能发现什么?『生』:建立直角坐标系有多种方法。2.【例】对于边长为4的整三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标。解:略(见书P138)。『师』:正三角形的边长已经确定是4,则它一边上的高是不是会因所处位置的不同而发生变化?『生』:不会,只是位置变化,而长度不会变。『师』:除了上面的直角坐标系的选取外,是否还有其他的选取方法?『生』:有,……3.议一议你认为怎样建立适合的直角坐标系?上面三个活动的目的:(1)体会不同的坐标系同一图形的位置不同,那么,关键点的坐标也不同。(2)确定坐标系时,一方面是看点的位置,同时也与此点到坐标轴有关,而距离往往需要进行计算。(3)培养学生综合应用知识解决问题的能力。4.回解情境问题(寻宝问题)教学处理:(1)让学生分组讨论如何找到宝藏。(2)让每组选一名代表...