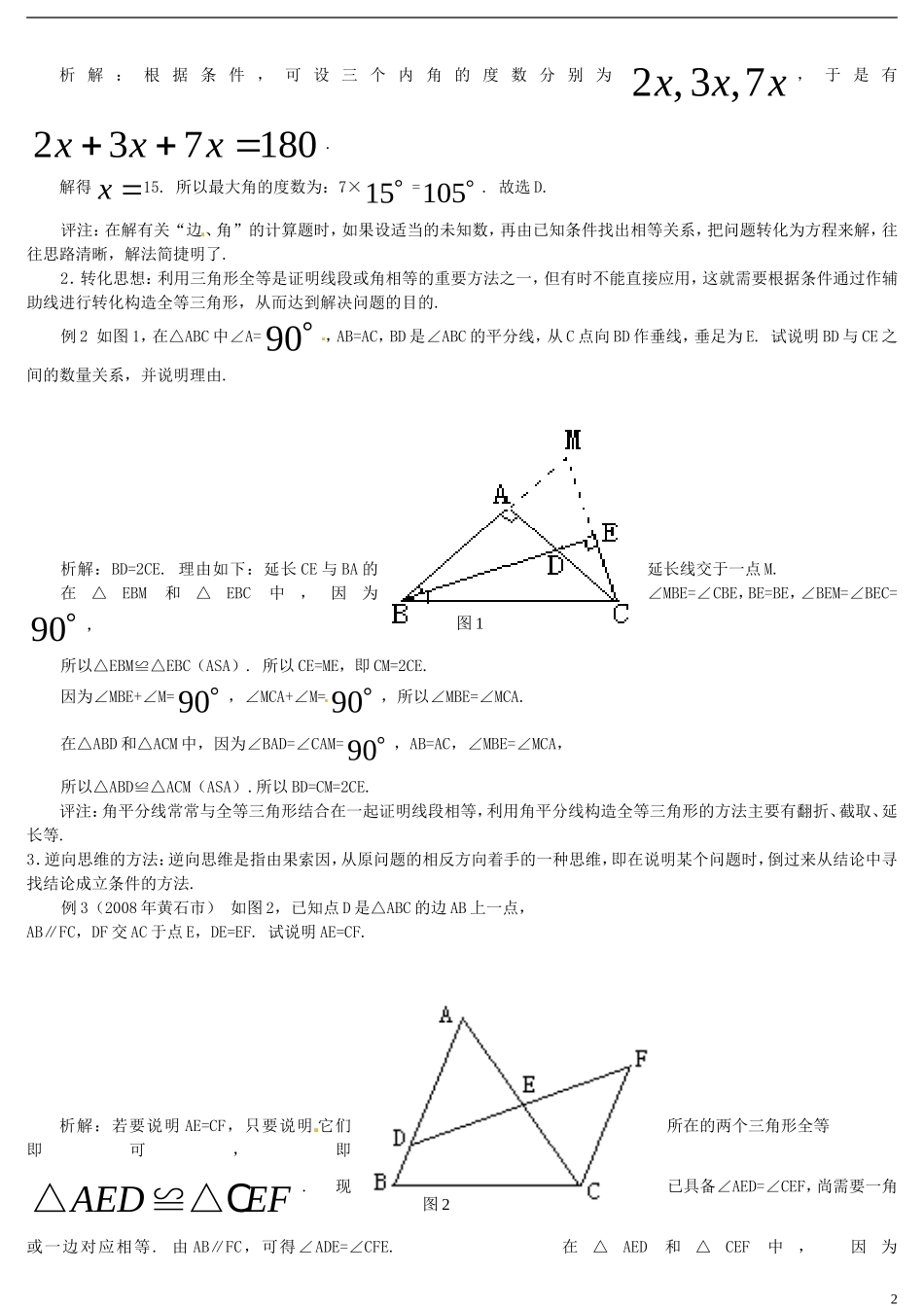
全等三角形综合指导一、基础知识回顾1.三角形的概念由___________的三条线段________相接所组成的图形叫做三角形,它有____条边和____个内角,三角形可用符号_______表示.2.三角形的三条重要线段(1)在三角形中,一个内角的平分线与它的对边相交,这个角的顶点和交点之间的线段叫做__________.三角形的三条角平分线一定在三角形的内部,且它们交于________.(2)在三角形中,连结一个顶点和它对边中点的线段,叫做__________.三角形的三条中线一定在三角形的内部,且它们交于________.(3)从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做______.在________三角形中,三条高在三角形的内部,因而交点也在三角形的内部;在________三角形中,只有一条高在三角形的内部,另外两条高恰好是三角形的两条直角边,因而交点正好是_________;在_______三角形中,有一条高在三角形的内部,另外两条高在三角形的外部,这三条高的延长线相交于________.3.三角形的有关性质:(1)三角形的任意两边之和______第三边,任意两边之差_____第三边.(2)三角形的内角和为________;直角三角形的两个锐角_______.(3)三角形具有________,即三角形的三边的长度确定后,其形状保持不变.4.三角形的分类(1)按______分类:直角三角形—等腰直角三角形三角形锐角三角形斜三角形钝角三角形(2)按______分类:不等边三角形三角形底边和腰不相等的等腰三角形等腰三角形等边三角形5.全等三角形的性质:全等三角形的________相等,________相等.6.三角形全等的判定(1)________对应相等的两个三角形全等,简记为“SSS”;(2)_____和_________对应相等的两个三角形全等,简记为“ASA”;(3)_____和_______对应相等的两个三角形全等,简记为“AAS”;(4)_____和_______对应相等的两个三角形全等,简记为“SAS”;7.直角三角形全等的判定直角三角形全等的判定除了可以利用SSS,ASA,AAS,SAS判定外,它还可以利用“HL”来判定,即_____和_______对应相等的两个直角三角形全等.8.三角形全等的应用:(1)利用尺规作图(2)利用三角形全等测量距离.二、主要思想方法1.方程思想:就是从分析问题的数量关系入手,通过设定未知数,把问题中的已知量与未知量的数量关系,转化为方程模型,使问题得到解决.例1(2008年陕西省)一个三角形三个内角的度数之比为2∶3∶7,这个三角形是().A.直角三角形B.等腰三角形C.锐角三角形D.钝角三角形1析解:根据条件,可设三个内角的度数分别为2,3,7xxx,于是有237180xxx.解得x15.所以最大角的度数为:7×15=105.故选D.评注:在解有关“边、角”的计算题时,如果设适当的未知数,再由已知条件找出相等关系,把问题转化为方程来解,往往思路清晰,解法简捷明了.2.转化思想:利用三角形全等是证明线段或角相等的重要方法之一,但有时不能直接应用,这就需要根据条件通过作辅助线进行转化构造全等三角形,从而达到解决问题的目的.例2如图1,在△ABC中∠A=90,AB=AC,BD是∠ABC的平分线,从C点向BD作垂线,垂足为E.试说明BD与CE之间的数量关系,并说明理由.析解:BD=2CE.理由如下:延长CE与BA的延长线交于一点M.在△EBM和△EBC中,因为∠MBE=∠CBE,BE=BE,∠BEM=∠BEC=90,所以△EBM≌△EBC(ASA).所以CE=ME,即CM=2CE.因为∠MBE+∠M=90,∠MCA+∠M=90,所以∠MBE=∠MCA.在△ABD和△ACM中,因为∠BAD=∠CAM=90,AB=AC,∠MBE=∠MCA,所以△ABD≌△ACM(ASA).所以BD=CM=2CE.评注:角平分线常常与全等三角形结合在一起证明线段相等,利用角平分线构造全等三角形的方法主要有翻折、截取、延长等.3.逆向思维的方法:逆向思维是指由果索因,从原问题的相反方向着手的一种思维,即在说明某个问题时,倒过来从结论中寻找结论成立条件的方法.例3(2008年黄石市)如图2,已知点D是△ABC的边AB上一点,AB∥FC,DF交AC于点E,DE=EF.试说明AE=CF.析解:若要说明AE=CF,只要说明它们所在的两个三角形全等即可,即AEDEF△≌△C.现已具备∠AED=∠CEF,尚需要一角或一边对应相等.由AB∥...