2015正弦函数、余弦函数的图象VIP免费

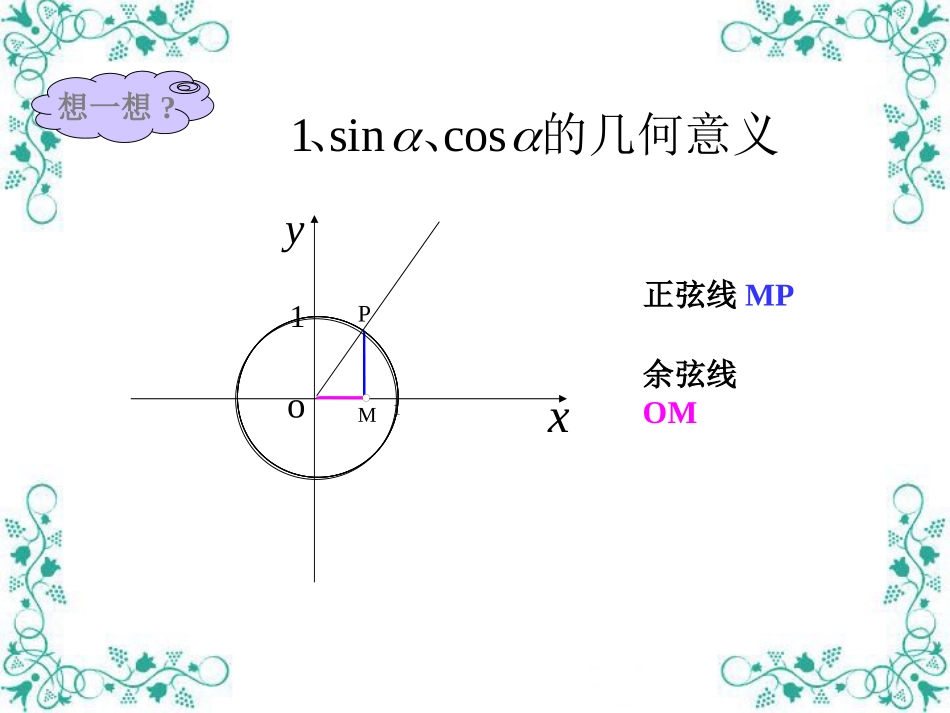
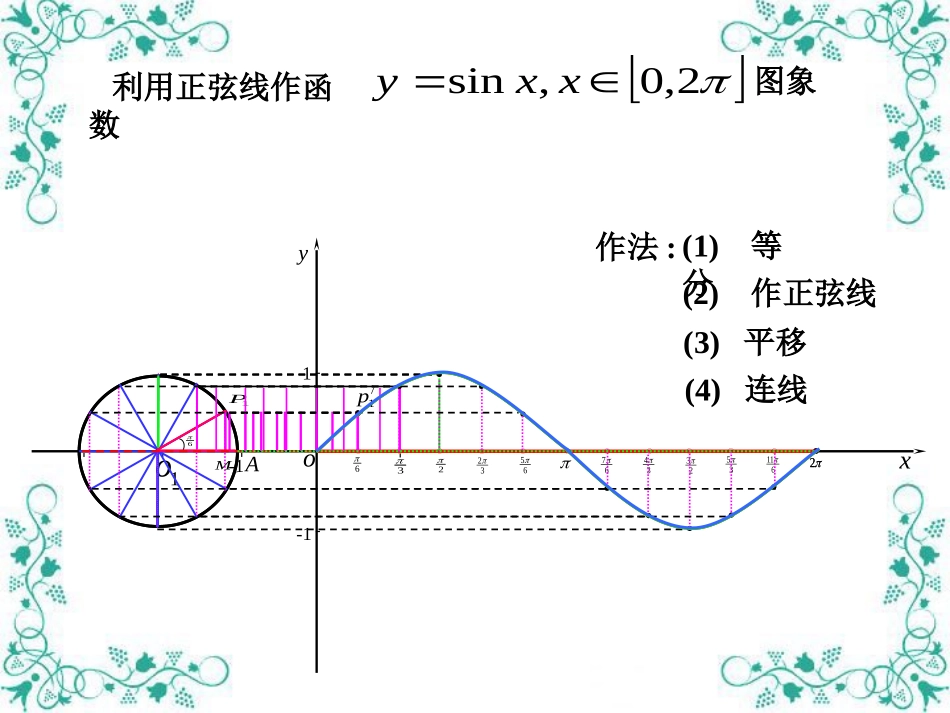
想一想?的几何意义、、cossin1oxy11PM正弦线MP余弦线OM利用正弦线作函数2,0,sinxxy图象作法:oxy---11---1--21oA3232656734233561126(2)作正弦线(3)平移61P1M/1p(4)连线(1)等分因为终边相同的角的三角函数值相同，所以y=sinx的图象在……，…与y=sinx,x[0,2π]∈的图象相同2,4,0,2,,2,0,4,2xy---------1-12o46246正弦曲线余弦曲线)cos(cosxxy)2sin()](2sin[xx由于所以余弦函数Rxxy,cos与函数Rxxy),2sin(是同一个函数；2余弦函数的图像可以通过正弦曲线向左平移各单位长度而得到．y--1-12o46246回忆描点法作出函数图象的主要步骤是怎样的？(1)列表2,0,sinxxyxy63232656734233561120212301212321230021231(2)描点---223xy0211---(3)连线图象的最高点)1,(2与x轴的交点)0,0()0,()0,2(图象的最低点)1(,23例1．画出下列函数的简图（1）y=sinx+1,x∈[0,2π]列表描点作图-2223211-xyo-xxsin1sinx101010210102232（2）y=－cosx,x∈[0,2π]解:（1）]2,0[,sin1xxy]2,0[,sinxxy2-22311xyo-（2）xxcosxcos0223210-101-1010-1]2,0[,cosxxy]2,0[,cosxxy练习：（1）作函数y=1+3cosx，x[0,2π]∈的简图（2）作函数y=2sinx-1，x[0,2π]∈的简图（1）yx小结:本节可主要学习了以下的内容（1）出利用单位圆中的三角函数线作Rxxy,sin的图象，明确图象的形状；)2sin(cosxxRxxy,cos（2）根据关系，作出的图象；（3）用“五点法”作出正弦函数、余弦函数的简图，并利用图象解决一些有关问题；