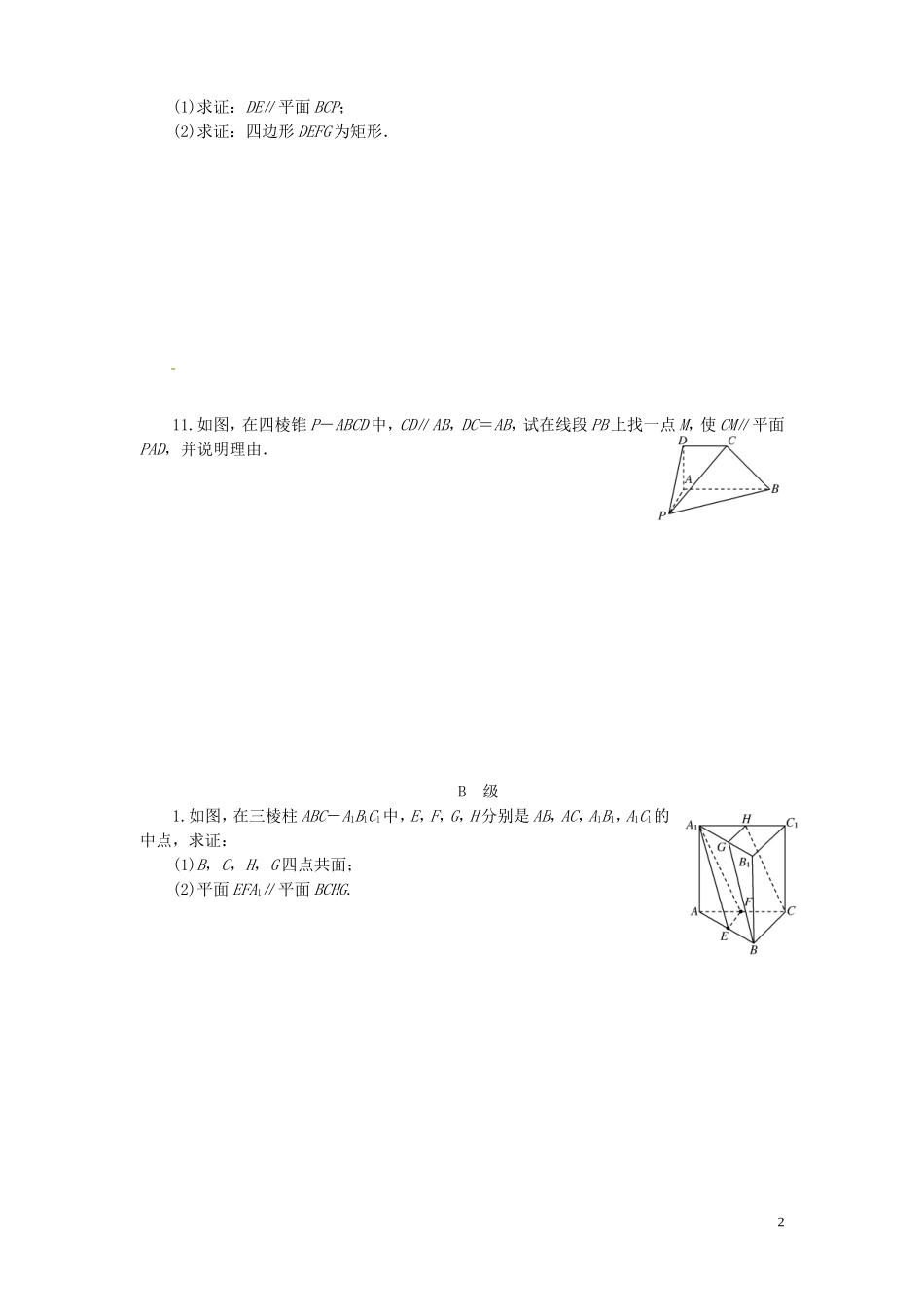
课时作业(四十二)直线、平面平行的判定及性质A级1.在梯形ABCD中,AB∥CD,AB⊂平面α,CD⊄平面α,则直线CD与平面α内的直线的位置关系只能是()A.平行B.平行和异面C.平行和相交D.异面和相交2.已知甲命题:“如果直线a∥b,那么a∥α”;乙命题:“如果a∥平面α,那么a∥b”.要使上面两个命题成立,需分别添加的条件是()A.甲:b⊂α;乙:b⊂αB.甲:b⊂α;乙:a⊂β且α∩β=bC.甲:a⊄α,b⊂α;乙:a⊂β且α∩β=bD.甲:a⊄α,b⊂α;乙:b∥α3.已知直线a∥平面α,如果平面α内有n条直线相交于一点,那么这n条直线中与直线a平行的()A.至少有一条B.至多有一条C.有且只有一条D.不可能有4.(2012·海口调研)平面α∥平面β的一个充分条件是()A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在两条平行直线a,b,a⊂α,b⊂β,a∥βD.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α5.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则()A.BD∥平面EFG,且四边形EFGH是平行四边形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是平行四边形D.EH∥平面ADC,且四边形EFGH是梯形6.在正方体的各面中,和其中一条棱平行的平面有________________________________________________________________________个.7.如图,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于________.8.如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为________.9.已知l,m,n是互不相同的直线,α,β,γ是三个不同的平面,给出下列命题:①若l与m为异面直线,l⊂α,m⊂β,则α∥β;②若α∥β,l⊂α,m⊂β,则l∥m;③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.其中所有真命题的序号为________.10.如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.1(1)求证:DE∥平面BCP;(2)求证:四边形DEFG为矩形.11.如图,在四棱锥P-ABCD中,CD∥AB,DC=AB,试在线段PB上找一点M,使CM∥平面PAD,并说明理由.B级1.如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EFA1∥平面BCHG.22.如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,且AB=2CD,在棱AB上是否存在一点F,使平面C1CF∥平面ADD1A1?若存在,求点F的位置;若不存在,请说明理由.答案:课时作业(四十二)A级1.B因为AB∥CD,AB⊂平面α,CD⊄平面α,所以CD∥平面α,所以CD与平面α内的直线可能平行,也可能异面,故选B.2.C根据直线与平面平行的判定定理和性质定理,知C正确.3.B可能存在也可能不存在,若存在只能是一条,因为若存在两条,则与平行公理相矛盾,所以选B.4.D选项A中的两平面可能平行,也可能相交;选项B中的平面可能平行也可能相交;选项C中的两个平面可能平行也可能相交;选项D,由a⊂α,a∥β,可知在β内存在直线a′∥a,所以a′∥α,又因为a,b异面,所以a′与b相交.又因为b∥α,所以α∥β.故选D.5.B如图,由题意,EF∥BD,且EF=BD.HG∥BD,且HG=BD.∴EF∥HG,且EF≠HG.∴四边形EFGH是梯形.又EF∥平面BCD,而EH与平面ADC不平行.故选B.6.解析:借助正方体的直观图易知,在正方体的六个面中,和其中一条棱平行的平面有两个.答案:27.解析: EF∥平面AB1C,EF⊂平面ADC,平面ADC∩平面AB1C=AC,∴EF∥AC,又 E为AD的中点,∴F为CD的中点,∴EF为△ADC的中位线,∴EF=AC,又正方体的棱长为2,∴AC=2,∴EF=AC=×2=.答案:8.解析:取PD的中点F,连接EF,3在△PCD中,EF綊CD.又 AB∥CD且CD=2AB,∴EF綊AB,∴四边形ABEF是平行四边形,∴EB∥AF.又 EB⊄平面PAD,AF⊂平面PAD,∴BE∥平面PAD.答案:平行9.解析:①中,当α,β不平行时,也可能存在符合条件的l,m;②中的直线l,m也可能异面;③中由l∥γ,l⊂β,γ∩...