信号系统在自动控制原理中的应用 VIP免费

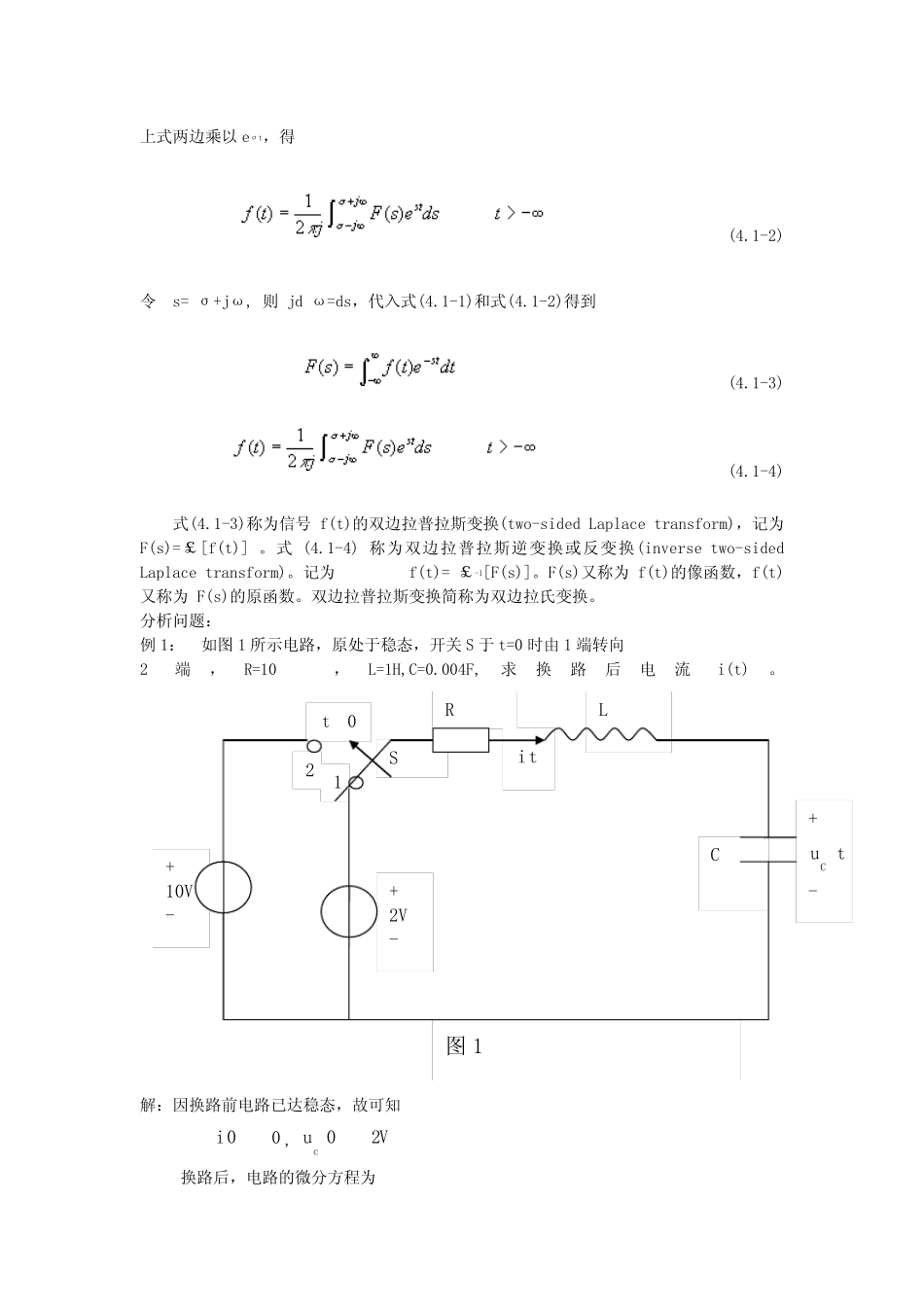
信号系统在自动控制原理中的应用【摘要】：信号系统的理论和方法在数学、自然科学和工程技术中有着广泛的应用，是解决诸如信号处理、通信系统、计算机系统、控制系统中的问题的有力工具。而自然科学和生产技术的发展又极大地推动了信号系统的发展，丰富了它的内容。我们在学习的过程中，要正确理解和掌握信号系统中的数学概念和方法，逐步培养利用这些概念和方法解决实际问题的能力。文中简单地介绍了该门课程在电气工程理论中的应用。【关键词】：线性系统卷积拉普拉斯变换【正文】：随着教育事业的不断发展与更新，一些新的处理数据的方法越来越多的应用于我们的日常专业学习中。当然信号系统在自动控制原理方面的应用也更大的加快了自动化的发展，自动控制也更加离不开一套有效的处理方法。但是常规的Fourier变换的运算的范围还是有限的，如何去解决一些不能展开成Fourier级数的信号成了我们的首要问题。而傅立叶变换和拉普拉斯变换又和信号有什么关系呢？傅立叶系数与波形对称性的关系一、为偶函数—纵轴对称即，如下图傅里叶系数：且有：二、为奇函数—原点对称即，如下图傅里叶系数：且有：从傅立叶变换到拉普拉斯变换：一个信号f(t)若满足绝对可积条件，则其傅里叶变换一定存在。例如，e-αtε(t)(α>0)就是这种信号。若f(t)不满足绝对可积条件，则傅里叶变换不一定存在。例如，信号ε(t)在引入冲激函数后其傅里叶变换存在，而信号eαtε(t)(α>0)的傅里叶变换不存在。若给信号eαtε(t)乘以信号e-σt(σ>α)，得到信号e-(σ-α)tε(t)。信号e-(σ-α)tε(t)满足绝对可积条件，因此其傅里叶变换存在。设有信号f(t)e-σt（σ为实数），并且能选择适当的σ使f(t)e-σt绝对可积,则该信号的傅里叶变换存在。若用F(σ+jω)表示该信号的傅里叶变换，根据傅里叶变换的定义，则有(4.1-1)根据傅里叶逆变换(inverseFouriertransform)的定义，则上式两边乘以eσt，得(4.1-2)令s=σ+jω,则jdω=ds，代入式(4.1-1)和式(4.1-2)得到(4.1-3)(4.1-4)式(4.1-3)称为信号f(t)的双边拉普拉斯变换(two-sidedLaplacetransform)，记为F(s)=￡[f(t)]。式(4.1-4)称为双边拉普拉斯逆变换或反变换(inversetwo-sidedLaplacetransform)。记为f(t)=￡-1[F(s)]。F(s)又称为f(t)的像函数，f(t)又称为F(s)的原函数。双边拉普拉斯变换简称为双边拉氏变换。分析问题：例1：如图1所示电路，原处于稳态，开关S于t=0时由1端转向2端，R=10，L=1H,C=0.004F,求换路后电流i(t)。解：因换路前电路已达稳态，故可知0i0,Vuc20换路后，电路的微分方程为图1+2V-+tuC-CLtiRS120t+10V-0cudttdiLtRitdiC0)(1=10)(t对上式进行拉普拉斯变换，得0issILsRIsCsIsuc)()0(=s10解得sI=sCsLRsuLisc1)0()0(10代入已知数据得sI=ssss25010210=2501082ss=2215)5(15158s用查表法可求得上式的拉普拉斯反变换为Attetit)(15sin1585例2：如图2所示为常用的二阶有源系统的电路模型，设1R、C=1F。试求系统函数（电压传递函数）sUsUsH12；当K=3时，求冲激响应th和阶跃响应ts。解：由图2可得s域的节点方程b1F+tu2-+tKub-+tub-1F1a1+tu1-图2sKUsURsUsUssCURsUsUsUsUsCRsUsUbbabbaaa221联立上述三式求解，并代入参数，可得13212sKsKsUsUsH当K=3时，得132ssH所以ttsHLthsin31V由于1312sssHssS故得阶跃响应tttscos13V由上面两例题可以看出，通过拉普拉斯变换可将时域中的微分方程变换为复频域中的代数方程，使求解简化。系统的起始状态（条件）可以自动地包含到象函数中，从而可一举求得方程的完全解。用拉普拉斯变换法分析电网络系统时，甚至不必列写出系统的微分方程，而直接利用电路的s域模型列写电路方程，就可以获得响应的象函数，再反变换即可得原函数。目前，卷积已成为现代电路与...